Next:
Gleichmäßigkeit. Gleichmäßige Konvergenz.
Up:
Analysis 2
Previous:
Die Methode der arithmetischen
Contents
Funktionenfolgen und -reihen. Parameterabhängige Integrale.
Subsections
Gleichmäßigkeit. Gleichmäßige Konvergenz.
Das Prinzip der Gleichmäßigkeit.
Punktweise und gleichmäßige Konvergenz von Funktionenfolgen.
Ein hinreichendes und notwendiges Kriterium für gleichmäßigen Konvergenz.
Gleichmäßig stetige Funktionen.
Weitere Definitionen.
Das Vertauschen von Grenzwerten
Problemstellung.
Der Satz über das Vertauschen von Grenzwerten.
Zur Stetigkeit der Grenzfunktion von Funktionenfolgen. Das Vertauschen der Grenzwerte
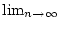und
.
Das Vertauschen der Grenzwerte
und
.
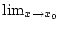Zur Stetigkeit der Grenzfunktion.
Die Stetigkeit der Grenzfunktion und die Vollständigkeit von
.
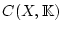Funktionenreihen und Grenzwerte.
Zur Stetigkeit von Funktionenreihen.
Eine Anwendung.
Zur Stetigkeit von Grenzwerten von Funktionen zweier Variablen. Das Vertauschen von
und
Das Vertauschen von Grenzwert und Integral
Zur Integration von Grenzfunktionen von Funktionenfolgen.
Zur Integration von Funktionenreihen.
Zum Vertauschen des Integralzeichens mit dem Grenzwert
.
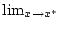Das kartesische Produkt metrischer Räume.
Zur Stetigkeit von parameterabhängigen Integralen.
Zum Vertauschen von Grenzwert und Ableitung
Die Differentation von Grenzfunktionen einer Funktionenfolge.
Die Differentation von Funktionenreihen.
Das Vertauschen von Ableitung und
.
Differenzieren und Integrieren von parameterabhängigen Integralen
Zur Differentation parameterabhängiger Integrale.
Die Integration parameterabhängiger Integrale.
Stetigkeit und Differenzierbarkeit von Integralen mit parameterabhängigen Integrationsgrenzen
Zur Formulierung des Problems.
Zur Stetigkeit.
Zur Differenzierbarkeit.
Zum Vertauschen von Grenzwerten mit uneigentlichen Integralen
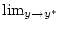Zur Konvergenz von Folgen uneigentlicher Intergrale.
Reihen uneigentlicher Integrale.
Parameterabhängige uneigentliche Integrale. Stetigkeit.
Parameterabhängige uneigentliche Integrale. Differenzierbarkeit bezüglich des Parameters.
Parameterabhängige uneigentliche Integrale. Integration bezüglich des Parameters.
Kriterien zur gleichmäßigen Konvergenz
Das Cauchy-Kriterium zur gleichmäßigen Konvergenz von Folgen.
Das Cauchy-Kriterium zur gleichmäßigen Konvergenz von Reihen.
Das Cauchy-Kriterium zur gleichmäßigen Konvergenz uneigentlicher Integrale.
Das Majorantenkriterium von Weierstrass.
Potenzreihen
Definition des Konvergenzkreises und der Konvergenzradiuses.
Der Satz von Cauchy und Hadamard.
Absolute und gleichmäßige Konvergenz von Potenzreihen.
Zur Differentation von Potenzreihen. Reelle Differenzierbarkeit.
Zur Differentation von Potenzreihen. Komplexe Differenzierbarkeit.
Die Taylorreihe.
Die Eulerschen Integrale
Die Betafunktion.
Wichtige Eigenschaften der Betafunktion.
Die Gammafunktion.
Der Zusammenhang zwischen der Beta- und der Gammafunktion.
Der Ergänzungssatz.
Der Verdoppelungssatz von Legendre.
Der Satz von Weierstrass und Stone
Die Formulierung des Satzes.
Zum Beweis von Satz 2.13.1.1.
2003-09-05
und
.
.
.
.