



Next: Parameterabhängige uneigentliche Integrale. Integration
Up: Zum Vertauschen von Grenzwerten
Previous: Parameterabhängige uneigentliche Integrale. Stetigkeit.
Contents
Satz 2.9.4.1
Die Funktion
![% latex2html id marker 26645
$ f\in C([a,b]\times [0,+\infty [\, ,\mathbb{R}) $](img1363.png) sei in allen Punkten
sei in allen Punkten
![$ (x,y)\in ]a,b[\, \times [0,+\infty [ $](img1364.png) partiell
nach
partiell
nach 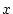 differenzierbar und
differenzierbar und
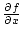 stetig auf
stetig auf
![$ [a,b]\times [0,+\infty [ $](img1365.png) fortsetzbar. Für alle
fortsetzbar. Für alle
![$ x\in [a,b] $](img1194.png) konvergiere das uneigentliche Integral
und desweiteren konvergiere das uneigentliche Integral
Dann ist
konvergiere das uneigentliche Integral
und desweiteren konvergiere das uneigentliche Integral
Dann ist 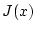 in
in ![$ ]a,b[ $](img1145.png) differenzierbar und es gilt
differenzierbar und es gilt
 Es sei
Es sei 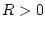 . Dann sind für die Funktion
die Voraussetzungen von Satz 2.7.1.1 erfüllt und es
gilt
Es sei
. Dann sind für die Funktion
die Voraussetzungen von Satz 2.7.1.1 erfüllt und es
gilt
Es sei 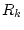 eine Folge positiver Zahlen mit der Eigenschaft
eine Folge positiver Zahlen mit der Eigenschaft
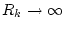 für
für
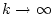 . Wir setzen
Dann konvergiert
. Wir setzen
Dann konvergiert
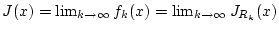 und
konvergiert gleichmäßig bezüglich
und
konvergiert gleichmäßig bezüglich
![$ x\in [a,b] $](img1194.png) . Nach Satz 2.6.1.1
gilt
. Nach Satz 2.6.1.1
gilt

2003-09-05
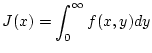
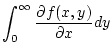
![$\displaystyle J^{\prime }(x)=\int _{0}^{\infty }\frac{\partial f(x,y)}{\partial x}dy,\quad x\in ]a,b[.$](img1368.png)
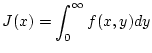
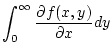
![$\displaystyle J^{\prime }(x)=\int _{0}^{\infty }\frac{\partial f(x,y)}{\partial x}dy,\quad x\in ]a,b[.$](img1368.png)
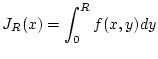
![$\displaystyle J_{R}^{\prime }(x)=\int _{0}^{R}\frac{\partial f(x,y)}{\partial x}dy,\quad x\in [a,b]\, .$](img1371.png)
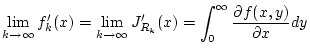
![$\displaystyle \int _{0}^{\infty }\frac{\partial f(x,y)}{\partial x}dy=\lim _{k\...
...ac{d}{dx}\lim _{k\to \infty }J_{R_{k}}(x)=\frac{dJ(x)}{dx},\quad x\in ]a,b[\, .$](img1376.png)