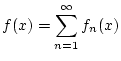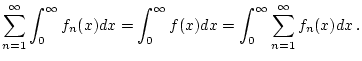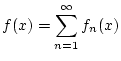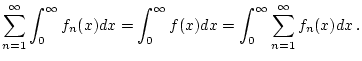Next: Parameterabhängige uneigentliche Integrale. Stetigkeit.
Up: Zum Vertauschen von Grenzwerten
Previous: Zur Konvergenz von Folgen
Contents
Satz 2.9.2.1
Wir betrachten eine Folge von Funktionen
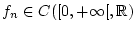 ,
,
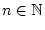 ,
so daß die uneigentlichen Integrale
,
so daß die uneigentlichen Integrale
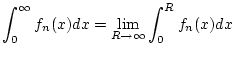  |
(2.9.2.1) |
konvergieren und außerdem für jedes fixierte
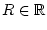 die Funktionenreihe
konvergiert. Dann existieren das uneigentliche Integral
die Funktionenreihe
konvergiert. Dann existieren das uneigentliche Integral
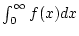 sowie die Reihe
sowie die Reihe
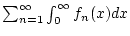 und es gilt
und es gilt
Aufgabe 2.9.2.2
Führen Sie Satz
2.9.2.1 selbständig auf Satz
2.9.1.1
zurück!
2003-09-05