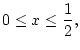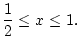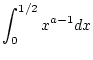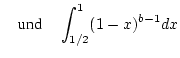Next: Wichtige Eigenschaften der Betafunktion.
Up: Die Eulerschen Integrale
Previous: Die Eulerschen Integrale
Contents
Für 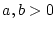 ist die Betafunktion gegeben durch die Formel
ist die Betafunktion gegeben durch die Formel
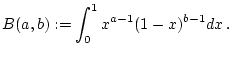 |
(2.12.1.1) |
Für 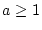 und
und 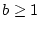 ist der Integrand eine beschränkte
Funktion und das obige Integral existiert im eigentlichen Sinn als
Riemann-Integral. Für
ist der Integrand eine beschränkte
Funktion und das obige Integral existiert im eigentlichen Sinn als
Riemann-Integral. Für 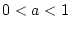 oder
oder 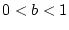 handelt es sich
bei (2.12.1.1) um ein konvergentes uneigentliches Integral.
Tatsächlich, es gilt
handelt es sich
bei (2.12.1.1) um ein konvergentes uneigentliches Integral.
Tatsächlich, es gilt
Die uneigentlichen Integrale
konvergieren für 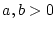 und damit konvergiert nach dem Vergleichskriterium
auch (2.12.1.1).
und damit konvergiert nach dem Vergleichskriterium
auch (2.12.1.1).
2003-09-05
![]() ist die Betafunktion gegeben durch die Formel
ist die Betafunktion gegeben durch die Formel