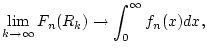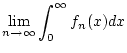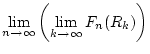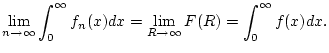Next: Reihen uneigentlicher Integrale.
Up: Zum Vertauschen von Grenzwerten
Previous: Zum Vertauschen von Grenzwerten
Contents
Satz 2.9.1.1
Wir betrachten eine Folge von Funktionen
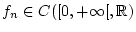 ,
,
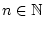 ,
so daß das uneigentliche Integral
,
so daß das uneigentliche Integral
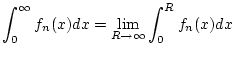  |
(2.9.1.1) |
konvergiert und außerdem für jedes fixierte
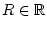 der Grenzwert
angenommen wird. Dann konvergiert das uneigentliche Integral
der Grenzwert
angenommen wird. Dann konvergiert das uneigentliche Integral
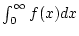 sowie der Grenzwert
sowie der Grenzwert
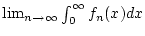 und es gilt
und es gilt
 Aufgrund der Stetigkeit von
Aufgrund der Stetigkeit von 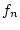 existiert für jedes
existiert für jedes 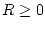 das Integral
Desweiteren ist
das Integral
Desweiteren ist 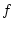 als gleichmäßiger Grenzwert (auf jedem beliebigen
endlichen Intervall) stetiger Funktionen selbst stetig. Damit existiert
für jedes
als gleichmäßiger Grenzwert (auf jedem beliebigen
endlichen Intervall) stetiger Funktionen selbst stetig. Damit existiert
für jedes 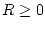 auch die Größe
Wiederum aufgrund der gleichmäßigen Konvergenz von
auch die Größe
Wiederum aufgrund der gleichmäßigen Konvergenz von 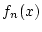 gegen
gegen 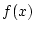 bezüglich
bezüglich
![$ x\in [0,R] $](img1319.png) folgt nach Satz 2.5.1.1
folgt nach Satz 2.5.1.1
Wir wählen nun eine Folge
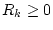 mit
mit
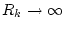 für
für
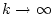 . Wegen (2.9.2.1) konvergiert
. Wegen (2.9.2.1) konvergiert
Dann folgt nach Satz 2.2.2.1
Da die linke Seite in dieser Identität nicht von der konkreten Wahl
der Folge
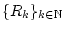 abhängt, so gilt auch
abhängt, so gilt auch





Next: Reihen uneigentlicher Integrale.
Up: Zum Vertauschen von Grenzwerten
Previous: Zum Vertauschen von Grenzwerten
Contents
2003-09-05
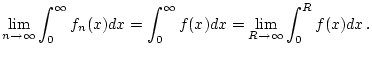
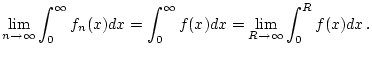
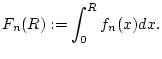
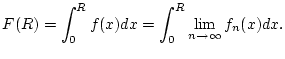
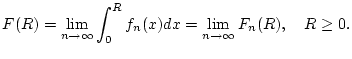
![]() mit
mit
![]() für
für
![]() . Wegen (2.9.2.1) konvergiert
. Wegen (2.9.2.1) konvergiert