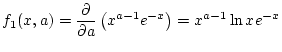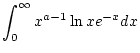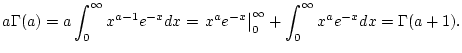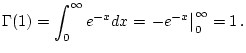Next: Der Zusammenhang zwischen der
Up: Die Eulerschen Integrale
Previous: Wichtige Eigenschaften der Betafunktion.
Contents
Für 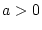 setzt man
setzt man
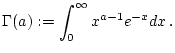 |
(2.12.3.1) |
Für 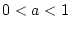 ist dies ein uneigentliches Integral an beiden Integrationsgrenzen,
für
ist dies ein uneigentliches Integral an beiden Integrationsgrenzen,
für 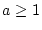 ist dies in der Umgebung von
ist dies in der Umgebung von 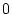 ein eigentliches
Integral.
ein eigentliches
Integral.
Aufgabe 2.12.3.1
: Zeigen Sie, daß für alle
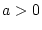
das uneigentliche Integral (
2.12.3.1)
konvergiert.
Wir untersuchen nun die Eigenschaften der Gammafunktion.
(I) Für alle 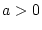 ist die Funktion
ist die Funktion
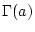 beliebig oft differenzierbar. Tatsächlich, wir betrachten einen Punkt
beliebig oft differenzierbar. Tatsächlich, wir betrachten einen Punkt
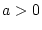 . Dann läßt sich die Funktion
. Dann läßt sich die Funktion
für
![$ a\in [a_{1},a_{2}] $](img1599.png) mit fixierten
mit fixierten
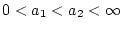 durch
abschätzen. Da das uneigentliche Integral
durch
abschätzen. Da das uneigentliche Integral
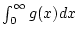 konvergiert2.6, so konvergiert nach dem Majorantenkriterium von Weierstrass das
uneigentliche Integral
Damit ist Satz 2.9.4.1 anwendbar und es gilt
Analog kann man auch die höhere Ableitungen berechnen2.7.
konvergiert2.6, so konvergiert nach dem Majorantenkriterium von Weierstrass das
uneigentliche Integral
Damit ist Satz 2.9.4.1 anwendbar und es gilt
Analog kann man auch die höhere Ableitungen berechnen2.7.
(II) Wir zeigen, daß
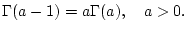 |
(2.12.3.2) |
Tatsächlich, durch partielle Integration folgt
Wendet man diese Formel wiederholt an, so ergibt sich
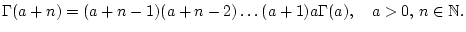 |
(2.12.3.3) |
Weiterhin gilt
Daraus folgt
Damit kann man die Gammafunktion als Verallgemeinerung der Fakultät
betrachten.
(III) Man sieht leicht, daß




Next: Der Zusammenhang zwischen der
Up: Die Eulerschen Integrale
Previous: Wichtige Eigenschaften der Betafunktion.
Contents
2003-09-05
![]() setzt man
setzt man![]() ist die Funktion
ist die Funktion
![]() beliebig oft differenzierbar. Tatsächlich, wir betrachten einen Punkt
beliebig oft differenzierbar. Tatsächlich, wir betrachten einen Punkt
![]() . Dann läßt sich die Funktion
. Dann läßt sich die Funktion