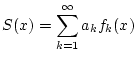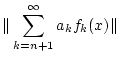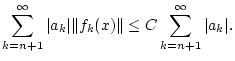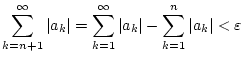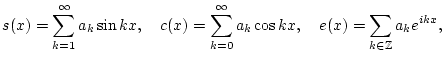Next: Zur Stetigkeit von Grenzwerten
Up: Zur Stetigkeit der Grenzfunktion
Previous: Zur Stetigkeit von Funktionenreihen.
Contents
Es sei 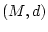 ein metrischer Raum und
ein metrischer Raum und
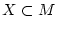 . Desweiteren
sei
. Desweiteren
sei
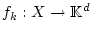 ,
,
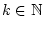 , eine
Familie von stetigen Funktionen, welche die gleichmäßige Abschätzung
, eine
Familie von stetigen Funktionen, welche die gleichmäßige Abschätzung
erfüllen. Wir betrachten eine Folge
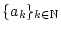 mit Gliedern
mit Gliedern
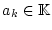 ,
,
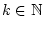 ,
so daß die Reihe
,
so daß die Reihe
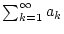 absolut konvergiert.
Dann konvergiert die Reihe
und damit ist nach Satz 2.3.5.1 die Funktion
absolut konvergiert.
Dann konvergiert die Reihe
und damit ist nach Satz 2.3.5.1 die Funktion 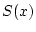 stetig. Tatsächlich, es gilt
stetig. Tatsächlich, es gilt
Aufgrund der absoluten Konvergenz der Reihe
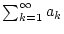 existiert also für gegebenes
existiert also für gegebenes
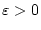 ein
ein
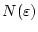 ,
so daß
und damit
was die gleichmäßige Konvergenz von
,
so daß
und damit
was die gleichmäßige Konvergenz von
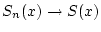 impliziert.
impliziert.
Der Leser kann die obige Beobachtung leicht zum Beweis für folgenden
wichtigen Spezialfall modifizieren:




Next: Zur Stetigkeit von Grenzwerten
Up: Zur Stetigkeit der Grenzfunktion
Previous: Zur Stetigkeit von Funktionenreihen.
Contents
2003-09-05
![]() ein metrischer Raum und
ein metrischer Raum und
![]() . Desweiteren
sei
. Desweiteren
sei
![]() ,
,
![]() , eine
Familie von stetigen Funktionen, welche die gleichmäßige Abschätzung
, eine
Familie von stetigen Funktionen, welche die gleichmäßige Abschätzung