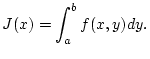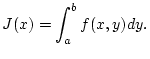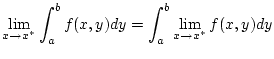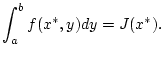Next: Zum Vertauschen von Grenzwert
Up: Das Vertauschen von Grenzwert
Previous: Das kartesische Produkt metrischer
Contents
 Die Menge
Die Menge
![$ X\times [a,b] $](img1132.png) ist nach Satz 2.5.4.2
in
ist nach Satz 2.5.4.2
in
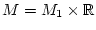 kompakt. Nach dem Satz von Cantor
ist die Funktion
kompakt. Nach dem Satz von Cantor
ist die Funktion
![% latex2html id marker 25649
$ f\in C(X\times [a,b],\mathbb{K}^{d}) $](img1134.png) gleichmäßig
stetig, d.h.
Damit wird für jedes
gleichmäßig
stetig, d.h.
Damit wird für jedes
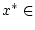
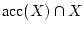 der Grenzwert
angenommen. Da für jedes
der Grenzwert
angenommen. Da für jedes 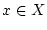 ist die Funktion
ist die Funktion
![% latex2html id marker 25661
$ f(x,\cdot ):[a,b]\to \mathbb{K}^{d} $](img1138.png) stetig in
stetig in
![$ y\in [a,b] $](img1101.png) . Nach Satz 2.5.3.1 und
der Stetigkeit von
. Nach Satz 2.5.3.1 und
der Stetigkeit von 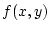 gilt
gilt
Also ist die Funktion 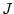 stetig.
stetig.

2003-09-05