Zum Beweis von Satz 2.13.1.1.

Wir folgend der Darstellung in [Rudin].

Schritt 1: Durch eine affine Koordinatentransformation, welche Polynome wieder in Polynome überführt, läßt sich das Problem stets auf das Intervall $[a,b]=[0,1]$ zurückführen. Desweiteren kann man o.B.d.A. annehmen, daß $f(0)=f(1)=0$ gilt, denn eine allgemeine Funktion $g\in C([a,b],\mathbb{C})$ kann man durch Subtraktion des Polynoms $u(x)=x(g(1)-g(0))+g(0)$ ersten Grades auf

$$f(x)=g(x)-u(x)$$$$\quad \mbox {mit}\quad f(0)=f(1)=0$$

zurückführen. Approximiert dann die Folge von Polynome $P_{n}$ die Funktion $f$, so konvergieren offensichtlich die Polynome $P_{n}+u$ gegen $f+u=g$.

Verschwindet die stetige Funktion $f$ am Rand des Intervalles $[0,1]$, so läßt sich sich stetig mit $f(x)=0$, $x\in \mathbb{R}\setminus [0,1]$ auf die gesamte reelle Achse fortsetzen. Nach dem Satz von Cantor ist $f$ auf $[0,1]$ gleichmäßig stetig ist, und offensichtlich bleibt bei dieser Fortsetzung auf die reelle Achse diese Funktion auch gleichmäßig stetig auf $\mathbb{R}$.

Schritt 2: Wir betrachten nun die Polynome

$$Q_{n}(x):=c_{n}(1-x^{2})^{n},\quad n\in \mathbb{N}.$$

Dabei seien die Koeffizienten $c_{n}$ so gewählt, daß

$$\int _{-1}^{1}Q_{n}(x)dx=1,\quad n\in \mathbb{N},$$

gilt. Dies ist immer möglich, da wegen $(1-x)^{2}>0$ für $x\in ]-1,1[$ das Integral $\int _{-1}^{1}(1-x^{2})^{n}dx$ stets einen positiven Wert annimmt, dabei gilt $c_{n}>0$ für alle $n\in \mathbb{N}$.

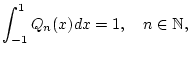
Wir benötigen im weiteren eine Abschätzung von oben an die Konstanten $c_{n}$. Dazu merken wir zunächst an, daß

$$(1-x^{2})\geq 1-nx^{2},\quad x\in [0,1],\quad n\in \mathbb{N},$$

was sofort aus $h(0)=0$ und $h^{\prime }(x)>0$ mit $h(x)=(1-x^{2})^{n}-1+nx^{2}$ für $x\in [0,1]$ folgt. Dann ergibt die Rechnung

$$\frac{1}{c_{n}}=\int _{-1}^{1}(1-x^{2})^{n}dx = 2\int _{0}^{1}(1-x^{2})^{n}dx\geq 2\int _{0}^{n^{-\frac{1}{2}}}(1-x^{2})^{n}dx\notag$$ (2.13.2.1)

$$\geq 2\int _{0}^{n^{-\frac{1}{2}}}(1-nx^{2})dx\notag$$ (2.13.2.2)

$$\stackrel{(y=\sqrt{n}x)}{=} \frac{2}{\sqrt{n}}\int _{0}^{1}(1-y^{2})dy=\frac{4}{3\sqrt{n}}>\frac{1}{\sqrt{n}}$$ (2.13.2.3)

die Ungleichung $c_{n}<\sqrt{n}$ für alle $n\in \mathbb{N}$.

Wir fixieren nun ein beliebiges $\delta \in \, ]0,1[$. Dann gilt für $\delta \leq \vert x\vert\leq 1$ und $q=1-\delta ^{2}\in \, ]0,1[$

$$0\leq Q_{n}(x)=c_{n}(1-x^{2})^{n}\leq \sqrt{n}(1-\delta ^{2})^{n}=\sqrt{n}q^{n}\stackrel{{n\to \infty }}{\to }0.$$ (2.13.2.4)

Mit anderen Worten konvergiert $Q_{n}(x)$ für $n\to \infty$ gleichmäßig gegen Null bezüglich $x\in [-1,-\delta ]\cup [\delta ,1]$ .

Schritt 3: Es sei $f(x)$ die in Schritt 1 betrachtete stetige Funktion, welche für $x\leq 0$ sowie für $x\geq 1$ verschwindet. Für $x\in [0,1]$ setzen wir

$$P_{n}(x) := \int _{-1}^{1}f(x+t)Q_{n}(t)dt\stackrel{x\in [0,1]}{=}\int _{-x}^{1-x}f(x+t)Q_{n}(t)dt$$

$$\stackrel{(\tilde{t}=x+t)}{=} \int _{0}^{1}f(\tilde{t})Q_{n}(\tilde{t}-x)d\tilde{t}=c_{n}\int _{0}^{1}f(\tilde{t})(1-(\tilde{t}-x)^{2})^{n}d\tilde{t}.$$

Da für jedes fixierte $\tilde{t}\in [0,1]$

$$(1-(\tilde{t}-x)^{2})^{n}=\sum _{k=0}^{2n}\beta _{k}(\tilde{t})x^{k}$$

ein Polynom in $x$ darstellt, so gilt

$$P_{n}(x)=c_{n}\sum _{k=0}^{2n}\alpha _{k}x^{k},\quad \alpha _{k}=\int _{0}^{1}f(\tilde{t})\beta _{k}(\tilde{t})d\tilde{t}\, .$$

Damit ist $P_{n}(x)$ ebenfalls ein Polynom in $x\in [0,1]$.

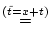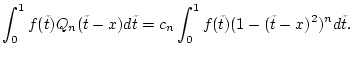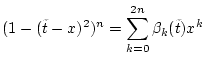
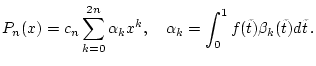
Schritt 4: Zunächst erinnern wir, daß nach Schritt 1 die Funktion $f$ auf $\mathbb{R}$ beschränkt und gleichmäßig stetig ist, d.h.

$$\forall _{\varepsilon >0}\exists _{\delta _{\varepsilon >0}}\forall _{\vert x-y\vert<\delta _{\varepsilon }}\, \vert f(x)-f(y)\vert<\varepsilon ,$$ (2.13.2.5)

$$M=\sup _{x\in \mathbb{R}}\vert f(x)\vert=\max _{x\in [0,1]}\vert f(x)\vert<\infty .$$ (2.13.2.6)

Wir schätzen nun die Differenz $P_{n}(x)-f_{n}(x)$ für $x\in [0,1]$ ab. Wegen $\int _{-1}^{1}Q_{n}(t)dt$ gilt

$$P_{n}(x)-f(x) = P_{n}(x)-f(x)\int _{-1}^{1}Q_{n}(t)dt$$

$$= \int _{-1}^{1}f(x+t)Q_{n}(t)dt-\int _{-1}^{1}f(x)Q_{n}(t)dt$$

und damit wegen $Q_{n}(t)\geq 1$ für $t\in [-1,1]$ auch

$$\vert P_{n}(x)-f(x)\vert\leq \int _{-1}^{1}\vert f(x+t)-f(x)\vert Q_{n}(t)dt\, ,\quad n\in \mathbb{N}.$$ (2.13.2.7)

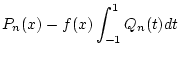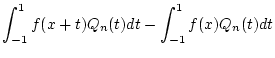Für ein beliebiges gegebenes $\varepsilon >0$ wählen wir nun nach (2.13.2.3) ein entsprechendes $\delta _{\varepsilon }\in ]0,1[\,$. Da nach (2.13.2.4) und (2.13.2.2)

$$\vert f(x+t)-f(x)\vert\leq 2M,\quad x\in [0,1],\quad t\in [-1,1]$$

sowie

$$0\leq Q_{n}(t)\leq \sqrt{n}q_{\varepsilon }^{n},\quad q_{\varepsi... ...\varepsilon }^{2})\in \, ]0,1[,\quad \vert t\vert\geq \delta >0_{\varepsilon },$$

gilt, so folgt

$$\int _{-1}^{-\delta _{\varepsilon }}\vert f(x+t)-f(x)\vert Q_{n}(t)dt \leq 2M\sqrt{n}q_{\varepsilon }^{n}\, ,$$ (2.13.2.8)

$$\int _{\delta _{\varepsilon }}^{1}\vert f(x+t)-f(x)\vert Q_{n}(t)dt \leq 2M\sqrt{n}q_{\varepsilon }^{n}\, ,$$ (2.13.2.9)

für alle $x\in [0,1]$. Da außerdem nach (2.13.2.3)

$$\vert f(x+t)-f(x)\vert\leq \varepsilon$$$$\quad \mbox {für}\quad \vert t\vert<\delta _{\varepsilon }<1,\quad x\in [0,1],$$

so gilt wiederum wegen $Q_{n}(t)\geq 0$ für $t\in [-1,1]$

$$\int _{-\delta _{\varepsilon }}^{\delta _{\varepsilon }}\vert f(x... ...arepsilon }}Q_{n}(t)dt\leq \varepsilon \int _{-1}^{1}Q_{n}(t)dt\leq \varepsilon$$ (2.13.2.10)

für beliebiges $x\in [0,1]$. Faßt man (2.13.2.5), (2.13.2.6), (2.13.2.7) und (2.13.2.8) zusammen, so erhält man schließlich die Abschätzung

$$\vert P_{n}(x)-f(x)\vert\leq 4M\sqrt{n}q_{\varepsilon }^{n}+\varepsilon ,\quad x\in [0,1],\quad n\in \mathbb{N}\, .$$

Dabei ist für gegebenes $\varepsilon >0$ der Wert von $q_{\varepsilon }\in \, ]0,1[$ unabhängig von $n$. Da $\sqrt{n}q_{\varepsilon }^{n}\to 0$ für $n\to \infty$, so kann man ein $N_{\varepsilon }\in \mathbb{N}$ so finden, daß $\sqrt{n}q^{n}_{\varepsilon }\leq 4^{-1}M^{-1}\varepsilon$ für $n\geq N_{\varepsilon }$ und damit

$$\vert P_{n}(x)-f(x)\vert\leq 2\varepsilon ,\quad x\in [0,1],\quad n\geq N_{\varepsilon }\, .$$

Damit konvergiert die Folge von Polynomen $P_{n}(x)$ gleichmäßig bezüglich $x\in [0,1]$ gegen $f(x)$.