



Next: Zur Differentation von Potenzreihen.
Up: Potenzreihen
Previous: Absolute und gleichmäßige Konvergenz
Contents
Lemma 2.11.4.1
Die Konvergenzradien der Potenzreihen
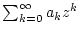 und
und
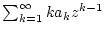 stimmen überein.
stimmen überein.
 Das Lemma folgt direkt aus der Formel für den Konvergenzradius in
Satz 2.11.2.1 sowie dem bekannten Grenzwert
Das Lemma folgt direkt aus der Formel für den Konvergenzradius in
Satz 2.11.2.1 sowie dem bekannten Grenzwert
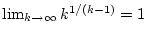 .
.

Als eine Folgerung aus diesem Lemma konvergieren beide Reihen
falls deren Konvergenzradius 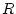 nicht verschwindet, im Inneren
ein und desselben Konvergenzkreises
nicht verschwindet, im Inneren
ein und desselben Konvergenzkreises 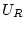 absolut als auch
in
absolut als auch
in
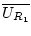 für beliebiges fixiertes
für beliebiges fixiertes 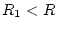 gleichmäßig. Nach Einschränkung auf die reelle Achse folgt aus Satz
2.6.2.1 sofort, daß die Funktion
gleichmäßig. Nach Einschränkung auf die reelle Achse folgt aus Satz
2.6.2.1 sofort, daß die Funktion 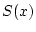 für
für
![$ x\in ]-R,R[ $](img1489.png) reell differenzierbar ist und
für alle
reell differenzierbar ist und
für alle
![% latex2html id marker 27238
$ x\in ]-R,R[\, =U_{R}\cap \mathbb{R} $](img1491.png) gilt. Damit kann
man in diesem Intervall die Potenzreihe
gilt. Damit kann
man in diesem Intervall die Potenzreihe
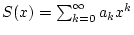 gliedweise reell differenzieren.
gliedweise reell differenzieren.
Das gleiche Argument kann man nun auf die Potenzreihe
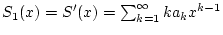 anwenden. Da sich dabei der Konvergenzradius nicht verändert, so läßt
sich diese Prozedur beliebig oft wiederholen. Damit ist die Funktion
anwenden. Da sich dabei der Konvergenzradius nicht verändert, so läßt
sich diese Prozedur beliebig oft wiederholen. Damit ist die Funktion
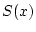 beliebig oft in
beliebig oft in
![$ x\in ]-R,R[ $](img1489.png) differenzierbar und
es gilt
differenzierbar und
es gilt
Die Potenzreihen der höheren Ableitungen besitzten dabei alle den
gleichen Konvergenzradius 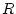 .
.




Next: Zur Differentation von Potenzreihen.
Up: Potenzreihen
Previous: Absolute und gleichmäßige Konvergenz
Contents
2003-09-05
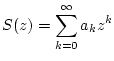
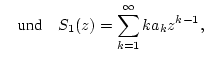
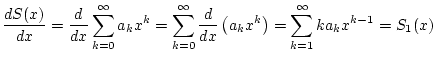
![]() anwenden. Da sich dabei der Konvergenzradius nicht verändert, so läßt
sich diese Prozedur beliebig oft wiederholen. Damit ist die Funktion
anwenden. Da sich dabei der Konvergenzradius nicht verändert, so läßt
sich diese Prozedur beliebig oft wiederholen. Damit ist die Funktion
![]() beliebig oft in
beliebig oft in
![]() differenzierbar und
es gilt
differenzierbar und
es gilt
![% latex2html id marker 27248
$\displaystyle \frac{d^{n}S(x)}{dx^{n}}=\sum _{k=n}^{\infty }a_{k}k(k-1)(k-n+1)x^{k-n},\quad x\in ]-R,R[,\quad n\in \mathbb{N}.$](img1494.png)