



Next: Funktionenreihen und Grenzwerte.
Up: Zur Stetigkeit der Grenzfunktion
Previous: Zur Stetigkeit der Grenzfunktion.
Contents
Die Stetigkeit der Grenzfunktion und die Vollständigkeit von
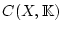 .
.
Im Punkt 2.15 des Skriptes zur Vorlesung Analysis 1 haben wir gezeigt,
daß für kompakte Mengen
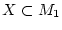 die Menge
die Menge
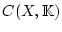 mit der Norm
mit der Norm
einen Banachraum bildet. Desweiteren haben wir dort auch gezeigt (vgl.
auch mit Satz 2.1.3.1), daß gleichmäßige Konvergenz
gleichbedeutend mit der Konvergenz in
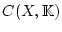 bezüglich
der Norm
bezüglich
der Norm
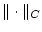 ist. Dann kann man Satz 2.3.2.1
für Funktionenfolgen
ist. Dann kann man Satz 2.3.2.1
für Funktionenfolgen
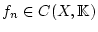 aus der Vollständigkeit
von
aus der Vollständigkeit
von
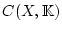 herleiten:
herleiten:
Wegen Satz 2.1.3.1 bedeutet die gleichmäßige Konvergenz
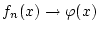 bezüglich
bezüglich 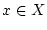 , daß
, daß
und damit
Nach dem Satz von Weierstrass gilt für die stetige Funktion
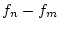 bei
bei
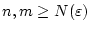 damit
d.h.
damit
d.h.
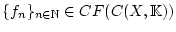 .
Damit existiert aufgrund der Vollständigkeit ein Grenzwert
.
Damit existiert aufgrund der Vollständigkeit ein Grenzwert
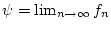 im Banachraum
im Banachraum
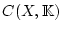 , d.h.
, d.h. 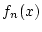 konvergiert
für
konvergiert
für
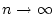 gleichmäßig bezüglich
gleichmäßig bezüglich 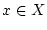 gegen
gegen
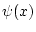 . Wegen der Eindeutigkeit des Grenzwertes
. Wegen der Eindeutigkeit des Grenzwertes
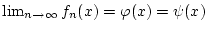 gilt damit
gilt damit
Es sei 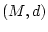 ein metrischer Raum,
ein metrischer Raum,
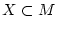 und
und
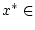
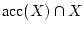 .
.




Next: Funktionenreihen und Grenzwerte.
Up: Zur Stetigkeit der Grenzfunktion
Previous: Zur Stetigkeit der Grenzfunktion.
Contents
2003-09-05
![]() die Menge
die Menge
![]() mit der Norm
mit der Norm
![]() bezüglich
bezüglich ![]() , daß
, daß
![]() ein metrischer Raum,
ein metrischer Raum,
![]() und
und
![]()
![]() .
.