



Next: Die Stetigkeit der Grenzfunktion
Up: Zur Stetigkeit der Grenzfunktion
Previous: Das Vertauschen der Grenzwerte
Contents
Wir betrachten die metrischen Räume
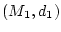 und
und
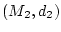 und es sei
und es sei
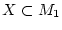 . Der metrische Raum
. Der metrische Raum 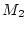 sei vollständig.
sei vollständig.
 Da
Da
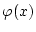 nach Definition in allen Punkten
nach Definition in allen Punkten
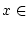
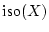 automatisch stetig ist, genügt es Punkte
automatisch stetig ist, genügt es Punkte
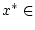
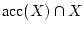 zu betrachten. Aus der Stetigkeit von
zu betrachten. Aus der Stetigkeit von 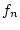 folgt dann
Nach Satz 2.3.1.1 gilt
folgt dann
Nach Satz 2.3.1.1 gilt
Damit ist 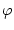 im Punkt
im Punkt 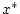 stetig.
stetig.

Sind die Funktionen 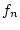 in allen Punkten
in allen Punkten 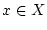 stetig,
so gilt gleiches auch für die Funktion
stetig,
so gilt gleiches auch für die Funktion 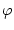 .
.
2003-09-05
![]() und
und
![]() und es sei
und es sei
![]() . Der metrische Raum
. Der metrische Raum ![]() sei vollständig.
sei vollständig.
![]() in allen Punkten
in allen Punkten ![]() stetig,
so gilt gleiches auch für die Funktion
stetig,
so gilt gleiches auch für die Funktion ![]() .
.