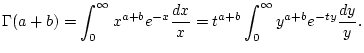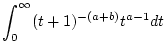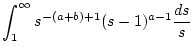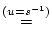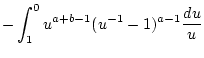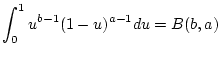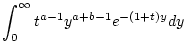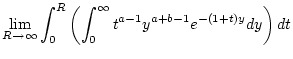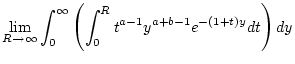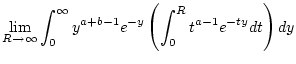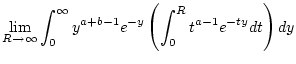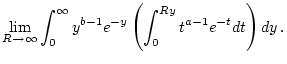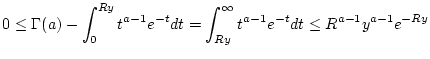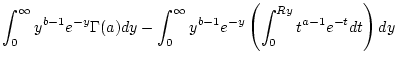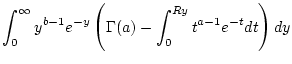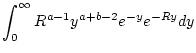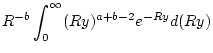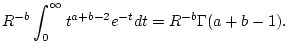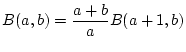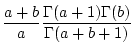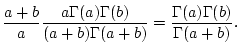Next: Der Ergänzungssatz.
Up: Die Eulerschen Integrale
Previous: Die Gammafunktion.
Contents
Substituiert man in der Definition (2.12.3.1) für 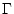 die Integrationsvariable
die Integrationsvariable 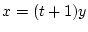 ,
, 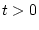 , so erhält man
, so erhält man
Daraus erhält man insbesondere
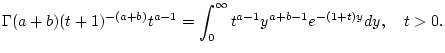 |
(2.12.4.1) |
Wir berechnen nun auf der linken und rechten Seite dieser Identität
das uneigentliche Integral
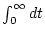 . Dazu merken
wir zunächst an, daß
. Dazu merken
wir zunächst an, daß
und damit auch
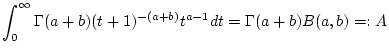 |
(2.12.4.2) |
gilt. Bei der Integration der rechten Seite von (2.12.4.1)
ist der Ausdruck
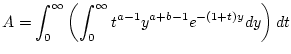 |
(2.12.4.3) |
zu berechnen. Wegen
und der Konvergenz von
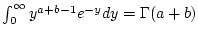 konvergiert das uneigentliche Integral
nach dem Majorantenkriterium gleichmäßig bezüglich
konvergiert das uneigentliche Integral
nach dem Majorantenkriterium gleichmäßig bezüglich
![$ t\in [\varepsilon ,R] $](img1629.png) für fixierte
für fixierte
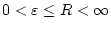 . Es sei zunächst
. Es sei zunächst
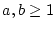 . Dann besitzt das zu untersuchende Integral (2.12.4.3)
nur eine Uneigentlichkeit in der Umgebung der unendlichen Integrationsgrenze.
Nach Satz 2.9.5.1 folgt
. Dann besitzt das zu untersuchende Integral (2.12.4.3)
nur eine Uneigentlichkeit in der Umgebung der unendlichen Integrationsgrenze.
Nach Satz 2.9.5.1 folgt
Weiterhin gilt
und damit auch für 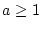 und
und 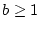
Daraus folgt
Die Gleichungen (2.12.4.2) und (2.12.4.4)
ergeben schließlich
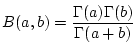 |
(2.12.4.6) |
für 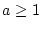 ,
,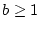 . Ist
. Ist 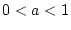 , so benutzen wir
nun (2.12.2.3) und (2.12.3.2) und erhalten
, so benutzen wir
nun (2.12.2.3) und (2.12.3.2) und erhalten
Auf gleichem Weg erweitert man Formel (2.12.4.5
) auch für 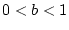 und damit auf alle
und damit auf alle 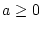 und
und 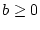 .
.




Next: Der Ergänzungssatz.
Up: Die Eulerschen Integrale
Previous: Die Gammafunktion.
Contents
2003-09-05
![]() die Integrationsvariable
die Integrationsvariable ![]() ,
, ![]() , so erhält man
, so erhält man