



Next: Zum Vertauschen von Grenzwerten
Up: Stetigkeit und Differenzierbarkeit von
Previous: Zur Stetigkeit.
Contents
 Es sei
Es sei
![$ x^{*}\in ]a,b[ $](img1290.png) . und wir verwenden die Zerlegung (2.8.2.1)-(2.8.2.4).
Nach Satz 2.7.1.1 ist die Funktion
. und wir verwenden die Zerlegung (2.8.2.1)-(2.8.2.4).
Nach Satz 2.7.1.1 ist die Funktion 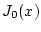 in
in
![$ x\in ]a,b[ $](img1173.png) differenzierbar und es gilt
An der Stelle
differenzierbar und es gilt
An der Stelle 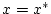 liefert dies den ersten Term auf der
rechten Seite von (2.8.3.1). Zur Untersuchung
der Differenzierbarkeit von
liefert dies den ersten Term auf der
rechten Seite von (2.8.3.1). Zur Untersuchung
der Differenzierbarkeit von 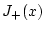 im Punkt
im Punkt 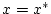 berechnen wir wegen
berechnen wir wegen
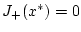 den Grenzwert
den Grenzwert
wobei
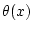 für gegebenes
für gegebenes
![$ x\in ]a,b[ $](img1173.png) nach dem ersten
Mittelwertsatz der Integralrechnung jeweils einen geeigneten Wert
zwischen
nach dem ersten
Mittelwertsatz der Integralrechnung jeweils einen geeigneten Wert
zwischen
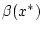 und
und 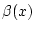 annimmt. Da
annimmt. Da 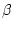 stetig ist, so existiert nach dem Satz von Bolzano und Cauchy ein
Punkt
stetig ist, so existiert nach dem Satz von Bolzano und Cauchy ein
Punkt
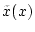 zwischen
zwischen 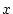 und
und 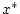 , so daß
, so daß
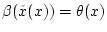 . Für
. Für
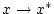 gilt
dann zwangsläufig
gilt
dann zwangsläufig
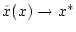 und wegen der Stetigkeit
von
und wegen der Stetigkeit
von 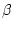 auch
auch
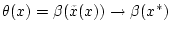 ,
so daß
Hier wurde ausgenutzt, daß zum einen
,
so daß
Hier wurde ausgenutzt, daß zum einen 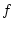 eine stetige Funktion
zweier Variablen ist und andererseits die Ableitung von
eine stetige Funktion
zweier Variablen ist und andererseits die Ableitung von 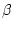 im Punkt
im Punkt 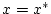 existiert. Dies entspricht dem zweiten Term
auf der rechten Seite von (2.8.3.1). Auf gleichem
Wege erhält man
was (2.8.3.1) vervollständigt.
existiert. Dies entspricht dem zweiten Term
auf der rechten Seite von (2.8.3.1). Auf gleichem
Wege erhält man
was (2.8.3.1) vervollständigt.

Satz 2.8.2.1 und Satz 2.8.3.1
kann man nun wie üblich schrittweise auf Funktionen mit Werten in
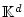 verallgemeinern.
verallgemeinern.




Next: Zum Vertauschen von Grenzwerten
Up: Stetigkeit und Differenzierbarkeit von
Previous: Zur Stetigkeit.
Contents
2003-09-05
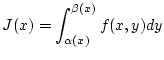
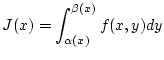
![$\displaystyle \frac{dJ_{0}(x)}{dx}=\int _{\alpha (x^{*})}^{\beta (x^{*})}\frac{\partial f(x,y)}{\partial x}dy,\quad x\in ]a,b[.$](img1291.png)
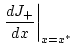
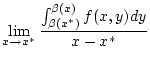
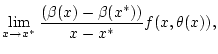
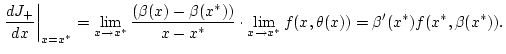
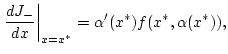
![]() verallgemeinern.
verallgemeinern.