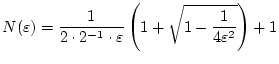Wir illustrieren dieses Prinzip am uns schon bekannten Beispiel der
punktweisen und der gleichmäßigen Konvergenz. Es sei ![]() ein metrischer Raum und wir betrachten eine Abbildung
ein metrischer Raum und wir betrachten eine Abbildung
![]() ,
d.h. eine Folge von Funktionen
,
d.h. eine Folge von Funktionen
![]() für
für
![]() .
.
Man sagt, daß diese Funktionenfolge punktweise konvergiert,
wenn für jedes ![]() die Folge der
die Folge der
![]() in
in
![]() konvergiert, d.h.
konvergiert, d.h.
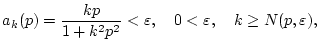
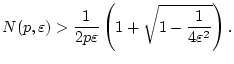
Betrachtet man hingegen die gleiche Folge ![]() bezüglich
einer anderen Parametermenge, z.B.
bezüglich
einer anderen Parametermenge, z.B.
![]() so kann man
so kann man