



Next: Gleichmäßig stetige Funktionen.
Up: Gleichmäßigkeit. Gleichmäßige Konvergenz.
Previous: Punktweise und gleichmäßige Konvergenz
Contents
 Angenommen es gilt (2.1.3.1), d.h.
Angenommen es gilt (2.1.3.1), d.h.
![% latex2html id marker 24329
$\displaystyle \forall _{\varepsilon >0}\exists _{...
...repsilon }}\left[ \sup _{p\in P}d(a_{k}(p),\alpha (p))<\varepsilon \right] \, .$](img816.png) |
(2.1.3.2) |
Aus
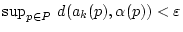 folgt
folgt
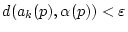 für alle
für alle 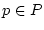 .
Demnach impliziert (2.1.3.2)
.
Demnach impliziert (2.1.3.2)
![% latex2html id marker 24339
$\displaystyle \forall _{\varepsilon >0}\exists _{...
..._{k\geq N_{\varepsilon }}\left[ d(a_{k}(p),\alpha (p))<\varepsilon \right] \, ,$](img819.png) |
(2.1.3.3) |
also liegt gleichmäßige Konvergenz vor.
Umgekehrt impliziert (2.1.3.3)
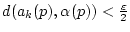 für alle
für alle 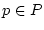 und
und
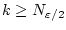 , und damit
, und damit
Dies ist gleichbedeutend mit (2.1.3.2), wenn
man
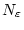 durch
durch
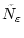 ersetzt.
ersetzt.

2003-09-05
![]() für alle
für alle ![]() und
und
![]() , und damit
, und damit