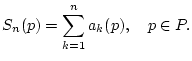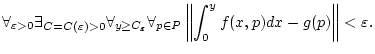Weitere Definitionen.

Wir sammeln hier einige weitere Definitionen, welche wir in diesem Punkt benötigen werden.

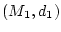
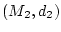
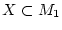
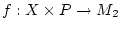
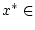
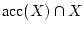
Definition 2.1.5.1   Es seien $(M_{1},d_{1})$ und $(M_{2},d_{2})$ metrische Räume sowie $X\subset M_{1}$. Wir betrachten eine Funktion $f:X\times P\to M_{2}$. Es sei $x^{*}\in$$\mbox {acc}(X)\cap X$. Wir sagen, daß der Grenzwert

$$g(p)=\lim _{x\to x^{*}}f(x,p)$$

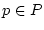
gleichmäßig bezüglich $p\in P$ erreicht wird, wenn folgende Aussage wahr ist

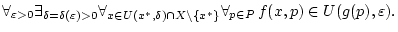$$\forall _{\varepsilon >0}\exists _{\delta =\delta (\varepsilon )>... ... )\cap X\setminus \{x^{*}\}}\forall _{p\in P}\, f(x,p)\in U(g(p),\varepsilon ).$$ (2.1.5.1)

Aufgabe 2.1.5.2   Es sei (2.1.5.1) erfüllt. Für eine gegebene Folge $\{x_{k}\}_{k\in \mathbb{N}}$ mit $x_{k}\in X$ und $x_{k}\to x^{*}$ für $k\to \infty$ setze man $f_{k}(p)=f(x_{k},p)$. Dann konvergiert $f_{k}(p)$ für $k\to \infty$ gleichmäßig gegen $g(p)$ bezüglich $p\in P$.

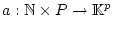
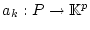
Definition 2.1.5.3   Es sei $a:\mathbb{N}\times P\to \mathbb{K}^{p}$ eine Folge von Abbildungen $a_{k}:P\to \mathbb{K}^{p}$. Wir betrachten die Partialsumme

$$S_{n}(p)=\sum _{k=1}^{n}a_{k}(p),\quad p\in P.$$

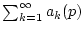
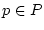
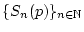
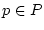
Man sagt, daß die Reihe $\sum _{k=1}^{\infty }a_{k}(p)$ gleichmäßig bezüglich $p\in P$ konvergiert genau dann, wenn die Folge $\{S_{n}(p)\}_{n\in \mathbb{N}}$ gleichmäßig bezüglich $p\in P$ konvergiert.

Als letzes betrachten wir die gleichmäßige Konvergenz uneigentlicher Integrale.

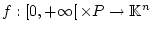
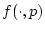
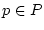
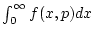
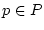
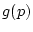
Definition 2.1.5.4   Es sei $f:[0,+\infty [\, \times P\to \mathbb{K}^{n}$ und $f(\cdot ,p)$ sei für jedes fixierte $p\in P$ auf jedem endlichen Intervall $[0,c]$ integrierbar. Das uneigentliche Integral $\int _{0}^{\infty }f(x,p)dx$ konvergiert gleichmäßig bezüglich $p\in P$ gegen $g(p)$ genau dann, wenn folgende Aussage gilt

$$\forall _{\varepsilon >0}\exists _{C=C(\varepsilon )>0}\forall _{... ...forall _{p\in P}\left\Vert \int _{0}^{y}f(x,p)dx-g(p)\right\Vert <\varepsilon .$$