



Next: Das Vertauschen von Grenzwert
Up: Funktionenfolgen und -reihen. Parameterabhängige
Previous: Eine Anwendung.
Contents
Es seien
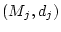 metrische Räume für
metrische Räume für 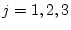 .
Insbesondere sei
.
Insbesondere sei 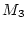 vollständig.
vollständig.
 Angenommen, der Grenzwert (2.4.0.1) wird gleichmäßig
erreicht. Wir betrachten eine beliebige Folge
Angenommen, der Grenzwert (2.4.0.1) wird gleichmäßig
erreicht. Wir betrachten eine beliebige Folge
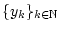 von Gliedern
von Gliedern
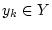 ,
,
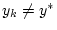 , welche für
, welche für
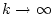 gegen
gegen 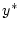 konvergiert uns setzen
konvergiert uns setzen
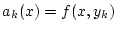 .
Nach Aufgabe 2.1.5.2 konvergiert
.
Nach Aufgabe 2.1.5.2 konvergiert 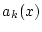 dann
für
dann
für
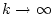 gleichmäßig bezüglich
gleichmäßig bezüglich 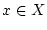 gegen
gegen
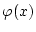 . Aus Satz 2.3.1.1 folgt
. Aus Satz 2.3.1.1 folgt
Da
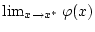 nicht von der konkreten Wahl
der Folge
nicht von der konkreten Wahl
der Folge
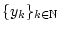 abhängt, so konvergiert
abhängt, so konvergiert
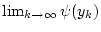 immer gegen ein und denselben
Wert, woraus nach der Folgendefiniton des Grenzwertes
folgt.
immer gegen ein und denselben
Wert, woraus nach der Folgendefiniton des Grenzwertes
folgt.

Satz 2.4.0.2
Unter den Voraussetzungen von Satz 2.4.0.2 sei
Dann ist
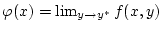 ebenfalls stetig
im Punkt
ebenfalls stetig
im Punkt 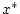 .
.
 Nach Satz 2.4.0.2 gilt
Aus der Stetigkeit von
Nach Satz 2.4.0.2 gilt
Aus der Stetigkeit von
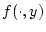 für fixiertes
für fixiertes 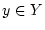 im Punkt
im Punkt 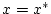 folgt
und damit
folgt
und damit

Wir erinnern, daß es zur Überprüfung der Stetigkeit genügt, Punkte
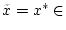
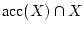 zu betrachten. Ist
deshalb unter den Vorassetzungen des obigen Satzes
zu betrachten. Ist
deshalb unter den Vorassetzungen des obigen Satzes
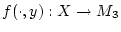 in allen Punkten
in allen Punkten 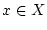 stetig, so gilt dies offensichtlich
auch für die Funktion
stetig, so gilt dies offensichtlich
auch für die Funktion
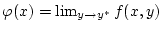 .
.




Next: Das Vertauschen von Grenzwert
Up: Funktionenfolgen und -reihen. Parameterabhängige
Previous: Eine Anwendung.
Contents
2003-09-05
![]() metrische Räume für
metrische Räume für ![]() .
Insbesondere sei
.
Insbesondere sei ![]() vollständig.
vollständig.
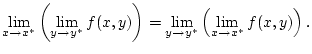
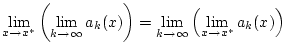
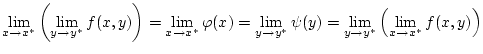
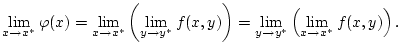
![]()
![]() zu betrachten. Ist
deshalb unter den Vorassetzungen des obigen Satzes
zu betrachten. Ist
deshalb unter den Vorassetzungen des obigen Satzes
![]() in allen Punkten
in allen Punkten ![]() stetig, so gilt dies offensichtlich
auch für die Funktion
stetig, so gilt dies offensichtlich
auch für die Funktion
![]() .
.