



Next: Absolute und gleichmäßige Konvergenz
Up: Potenzreihen
Previous: Definition des Konvergenzkreises und
Contents
Satz 2.11.2.1
Jede Potenzreihe
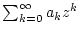 mit
mit
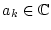 und
und
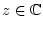 besitzt
einen Konvergenzkreis mit dem Konvergenzradius
besitzt
einen Konvergenzkreis mit dem Konvergenzradius
 Wir wenden auf
Wir wenden auf
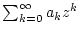 das Wurzelkriterium
von Cauchy zur Konvergenz von Reihen in der Limesform an. Ist
das Wurzelkriterium
von Cauchy zur Konvergenz von Reihen in der Limesform an. Ist
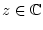 mit
mit 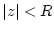 , dann gilt
Damit konvergiert nach Satz 1.5.3.1 die Reihe
, dann gilt
Damit konvergiert nach Satz 1.5.3.1 die Reihe
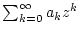 .
.
Umgekehrt liefert die gleiche Rechnung
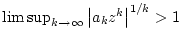 für
für 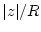 und damit nach Satz 1.5.3.1 die
Divergenz.
und damit nach Satz 1.5.3.1 die
Divergenz.

Man beachte, daß dieser Satz keine Aussage zur Konvergenz für 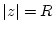 liefert.
liefert.
2003-09-05
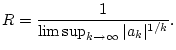
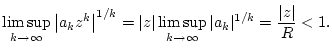
![]() für
für ![]() und damit nach Satz 1.5.3.1 die
Divergenz.
und damit nach Satz 1.5.3.1 die
Divergenz.
![]()
![]() liefert.
liefert.