



Next: Zur Stetigkeit der Grenzfunktion.
Up: Zur Stetigkeit der Grenzfunktion
Previous: Zur Stetigkeit der Grenzfunktion
Contents
Wir betrachten die metrischen Räume
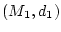 und
und
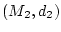 und es sei
und es sei
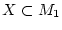 sowie
sowie
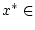
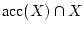 .
Der metrische Raum
.
Der metrische Raum 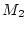 sei vollständig.
sei vollständig.
Satz 2.3.1.1
Es sei
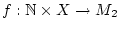 eine Folge von Funktionen
eine Folge von Funktionen
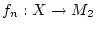 ,
,
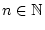 ,
so daß der Grenzwert
angenommen wird. Desweiteren konvergiere
Dann existieren die beiden Grenzwerte
,
so daß der Grenzwert
angenommen wird. Desweiteren konvergiere
Dann existieren die beiden Grenzwerte
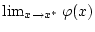 und
und
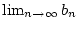 und es gilt
und es gilt
 Es sei
Es sei
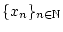 eine beliebige Folge von
Gliedern
eine beliebige Folge von
Gliedern
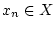 ,
,
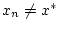 , welche für
, welche für
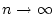 gegen
gegen 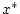 konvergiert.2.3 Es sei
konvergiert.2.3 Es sei
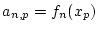 mit
mit
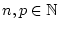 .
Dann konvergiert
wobei der erste dieser beiden Grenzwerte nach der Voraussetzung des
Satzes gleichmäßig bezüglich
.
Dann konvergiert
wobei der erste dieser beiden Grenzwerte nach der Voraussetzung des
Satzes gleichmäßig bezüglich
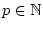 angenommen wird.
Nach Satz 2.2.2.1 konvergieren damit die Grenzwerte
Da die rechte Seite in dieser Identität nicht von der konkreten Wahl
der Folge
angenommen wird.
Nach Satz 2.2.2.1 konvergieren damit die Grenzwerte
Da die rechte Seite in dieser Identität nicht von der konkreten Wahl
der Folge
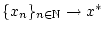 , abhängt, so
gilt nach der Folgendefinition der Konvergenz auch
, abhängt, so
gilt nach der Folgendefinition der Konvergenz auch





Next: Zur Stetigkeit der Grenzfunktion.
Up: Zur Stetigkeit der Grenzfunktion
Previous: Zur Stetigkeit der Grenzfunktion
Contents
2003-09-05
![]() und
und
![]() und es sei
und es sei
![]() sowie
sowie
![]()
![]() .
Der metrische Raum
.
Der metrische Raum ![]() sei vollständig.
sei vollständig.