



Next: Stetigkeit und Differenzierbarkeit von
Up: Differenzieren und Integrieren von
Previous: Zur Differentation parameterabhängiger Integrale.
Contents
Wir geben eine Skizze des Beweises dieses Satzes. Für Notationen verweisen
wir auf Kapitel 4.1 des Skriptes Analysis I. Wir empfehlen dem interessierten
Leser, die Details des Beweises auszuarbeiten.
 Wir betrachten zunächst reellwertige Funktionen und setzen
Wir betrachten zunächst reellwertige Funktionen und setzen
Nach Satz 2.5.5.1 sind
![% latex2html id marker 26027
$ I:[c,d]\to \mathbb{K}^{d} $](img1225.png) und
und
![% latex2html id marker 26029
$ J:[a,b]\to \mathbb{K}^{d} $](img1226.png) stetige Funktionen und damit
integrierbar.
stetige Funktionen und damit
integrierbar.
Es sei 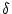 eine Zerlegungen des Intervalls
eine Zerlegungen des Intervalls ![$ [a,b] $](img87.png) und
und 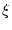 ein entsprechender Satz von Stützstellen. Für jedes
ein entsprechender Satz von Stützstellen. Für jedes
![$ y\in [c,d] $](img1229.png) gilt
gilt
wobei 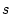 und
und 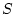 für die untere und die obere Darboux-Summe
und die Bezeichnung
für die untere und die obere Darboux-Summe
und die Bezeichnung
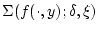 für die
entsprechende Riemann-Summe stehen. Ist
das Stetigkeitsmodul der Funktion
für die
entsprechende Riemann-Summe stehen. Ist
das Stetigkeitsmodul der Funktion
![% latex2html id marker 26060
$ f(\cdot ,y):[a,b]\to \mathbb{K} $](img1237.png) auf dem
auf dem 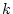 -ten Intervall
-ten Intervall
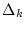 der Länge
der Länge
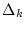 einer Zerlegung
einer Zerlegung 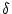 , so gilt
Da
, so gilt
Da 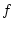 gleichmäßig stetig auf der kompakten Menge
gleichmäßig stetig auf der kompakten Menge
![$ [a,b]\times [c,d] $](img1198.png) ist, so existiert für jedes
ist, so existiert für jedes
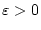 ein
ein
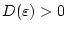 ,
so daß
Dies impliziert
,
so daß
Dies impliziert
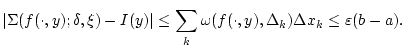 |
(2.7.2.1) |
Es sei nun
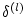 eine Folge von Zerlegungen mit der
Eigenschaft
eine Folge von Zerlegungen mit der
Eigenschaft
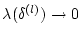 für
für
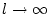 und
und
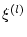 sei eine entsprechende Folge von Stützstellen.
Aus (2.7.2.1) folgt, daß der Grenzwert
sei eine entsprechende Folge von Stützstellen.
Aus (2.7.2.1) folgt, daß der Grenzwert
angenommen wird. Dann folgt nach Satz 2.5.1.1
Hierbei haben wir ausgenutzt, das bei fixiertem 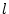 nur über
endlich viele Stützstellen
nur über
endlich viele Stützstellen
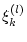 summiert wird und
daß damit diese endliche Summe
summiert wird und
daß damit diese endliche Summe 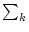 problemlos mit dem
Integral
problemlos mit dem
Integral
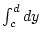 vertauscht werden kann.
vertauscht werden kann.
Abschließend kann man das zunächst für reellwertige Funktionen bewiesene
Resultat zunächst auf Funktionen mit Werten in
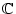 und dann auf Werte in
und dann auf Werte in
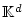 ausgeweitet werden.
ausgeweitet werden.





Next: Stetigkeit und Differenzierbarkeit von
Up: Differenzieren und Integrieren von
Previous: Zur Differentation parameterabhängiger Integrale.
Contents
2003-09-05
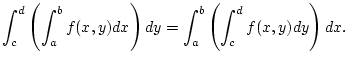
![]() Wir betrachten zunächst reellwertige Funktionen und setzen
Wir betrachten zunächst reellwertige Funktionen und setzen
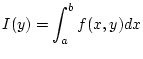
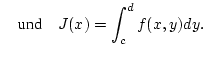
![]() eine Zerlegungen des Intervalls
eine Zerlegungen des Intervalls ![]() und
und ![]() ein entsprechender Satz von Stützstellen. Für jedes
ein entsprechender Satz von Stützstellen. Für jedes
![]() gilt
gilt
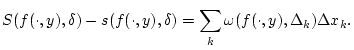
![]() eine Folge von Zerlegungen mit der
Eigenschaft
eine Folge von Zerlegungen mit der
Eigenschaft
![]() für
für
![]() und
und
![]() sei eine entsprechende Folge von Stützstellen.
Aus (2.7.2.1) folgt, daß der Grenzwert
sei eine entsprechende Folge von Stützstellen.
Aus (2.7.2.1) folgt, daß der Grenzwert
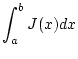
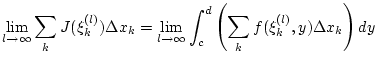
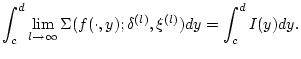
![]() und dann auf Werte in
und dann auf Werte in
![]() ausgeweitet werden.
ausgeweitet werden.
![]()