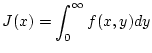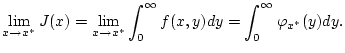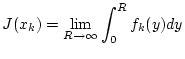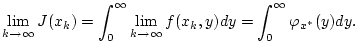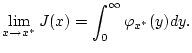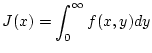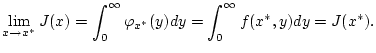Next: Parameterabhängige uneigentliche Integrale. Differenzierbarkeit
Up: Zum Vertauschen von Grenzwerten
Previous: Reihen uneigentlicher Integrale.
Contents
Es sei 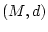 ein metrischer Raum und
ein metrischer Raum und
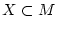 sowie
sowie
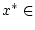
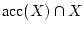 .
.
Satz 2.9.3.1
Für
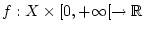 sei für jedes fixierte
sei für jedes fixierte 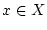 die Funktion
die Funktion
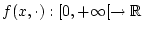 stetig in
stetig in 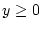 . Wir nehmen an, daß das uneigentliche Integral
konvergiert und für jedes fixierte
. Wir nehmen an, daß das uneigentliche Integral
konvergiert und für jedes fixierte 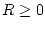 der Grenzwert
der Grenzwert
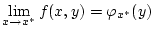 ![% latex2html id marker 26550
$\displaystyle \quad \mbox {gleichmäßig\, bezüglich}\quad y\in [0,R]$](img1344.png) |
(2.9.3.1) |
angenommen wird. Dann existiert der Grenzwert
 Man wähle eine Folge
Man wähle eine Folge
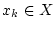 ,
,
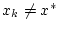 ,
,
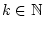 mit der Eigenschaft
mit der Eigenschaft
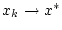 für
für
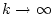 und setze
und setze
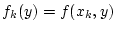 ,
, 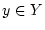 . Dann konvergiert
. Dann konvergiert
In der letzten Gleichung ist 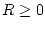 beliebig aber fixiert.
Aus Satz 2.9.1.1 folgt
Dieser Ausdruck ist unabhängig von der Wahl der Folge
beliebig aber fixiert.
Aus Satz 2.9.1.1 folgt
Dieser Ausdruck ist unabhängig von der Wahl der Folge 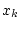 und demnach gilt
und demnach gilt

 Es sei
Es sei
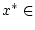
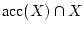 . Die Funktion
. Die Funktion 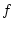 ist gleichmäßig stetig auf der kompakten Menge
ist gleichmäßig stetig auf der kompakten Menge
![$ X\times [0,R] $](img1360.png) und damit ist (2.9.3.1) mit
und damit ist (2.9.3.1) mit
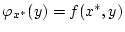 erfüllt. Aus Satz 2.9.3.1 folgt
erfüllt. Aus Satz 2.9.3.1 folgt





Next: Parameterabhängige uneigentliche Integrale. Differenzierbarkeit
Up: Zum Vertauschen von Grenzwerten
Previous: Reihen uneigentlicher Integrale.
Contents
2003-09-05
![]() ein metrischer Raum und
ein metrischer Raum und
![]() sowie
sowie
![]()
![]() .
.