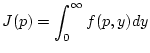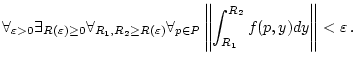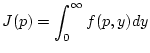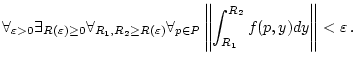Next: Das Majorantenkriterium von Weierstrass.
Up: Kriterien zur gleichmäßigen Konvergenz
Previous: Das Cauchy-Kriterium zur gleichmäßigen
Contents
Satz 2.10.3.1
Für die Funktion
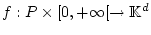 sei für alle fixierten
sei für alle fixierten 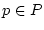 die Abbildung
die Abbildung
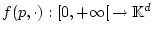 auf jedem endlichen Intervall
auf jedem endlichen Intervall ![$ [0,R] $](img1411.png) integrierbar. Das uneigentliche
Integral
genau dann, wenn folgende Aussage wahr ist
integrierbar. Das uneigentliche
Integral
genau dann, wenn folgende Aussage wahr ist
Aufgabe 2.10.3.2
Beweisen Sie diesen Satz selbständig!
2003-09-05