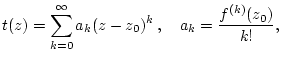Next: Die Eulerschen Integrale
Up: Potenzreihen
Previous: Zur Differentation von Potenzreihen.
Contents
Es sei
![% latex2html id marker 27333
$ f:\, ]-R,R[\, \to \mathbb{C} $](img1510.png) ,
, 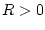 , eine im Punkt
, eine im Punkt
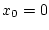 beliebig oft reell differenzierbare Funktion. Die Taylorsche
Formel bezüglich des Punktes
beliebig oft reell differenzierbare Funktion. Die Taylorsche
Formel bezüglich des Punktes 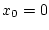 sagt aus, daß
sagt aus, daß
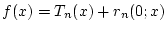 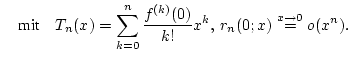 |
(2.11.6.1) |
Dies erlaubt eine Approximation von 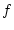 bis auf eine beliebig
vorgegebene Ordnung
bis auf eine beliebig
vorgegebene Ordnung 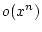 durch ein Polynom
durch ein Polynom 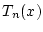 für
für 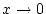 . Auf der anderen Seite bedeutet dies aber nicht,
daß die Partialsummen
. Auf der anderen Seite bedeutet dies aber nicht,
daß die Partialsummen 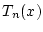 auch nur für ein bestimmtes
fixiertes
auch nur für ein bestimmtes
fixiertes 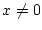 konvergieren muß.
konvergieren muß.
Betrachten wir die sogenannte Taylorreihe
genauer. Besitzt diese Potenzreihe einen positiven Konvergenzradius
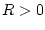 , so konvergiert diese Reihe
, so konvergiert diese Reihe
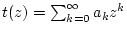 für alle komplexen
für alle komplexen 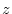 mit
mit 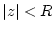 . Dann ist die Funktion
. Dann ist die Funktion
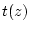 nach Satz 2.11.5.1 insbesondere
beliebig oft im Punkt
nach Satz 2.11.5.1 insbesondere
beliebig oft im Punkt 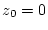 komplex differenzierbar. Formel
(2.11.5.1) gibt dann
Damit stimmen die Taylorkoeffizienten der Funktion
komplex differenzierbar. Formel
(2.11.5.1) gibt dann
Damit stimmen die Taylorkoeffizienten der Funktion 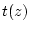 im
Punkt
im
Punkt 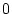 mit denen der Funktion
mit denen der Funktion 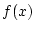 im Punkt
im Punkt 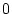 überein; beide Funktionen besitzen bezüglich des Punktes
überein; beide Funktionen besitzen bezüglich des Punktes 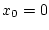 ein und dieselbe Taylorentwicklung.
ein und dieselbe Taylorentwicklung.
Wir unterstreichen, das letzteres nicht notwendigerweise bedeutet,
daß die Funktionen 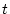 und
und 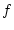 auf ihrem gemeinsamen Definitionsbereich
übereinstimmen. Als Beispiel betrachte man die Funktion
auf ihrem gemeinsamen Definitionsbereich
übereinstimmen. Als Beispiel betrachte man die Funktion
Man verifiziert leicht, daß 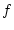 im Punkt
im Punkt 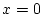 beliebig
oft reell differenzierbar ist und dabei
gilt. Damit ergibt sich die entsprechende Taylorreihe
beliebig
oft reell differenzierbar ist und dabei
gilt. Damit ergibt sich die entsprechende Taylorreihe 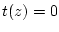 für alle
für alle
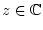 , was für reelle Argumente offensichtlich
nicht mit der Funktion
, was für reelle Argumente offensichtlich
nicht mit der Funktion 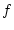 übereinstimmt.
übereinstimmt.
Aus (2.11.6.1) sieht man hingegen, daß
genau dann gilt, wenn
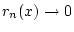 für
für
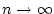 .
In diesem Fall sagt man, daß sich die Funktion
.
In diesem Fall sagt man, daß sich die Funktion 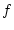 im Punkt
im Punkt 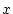 durch seine Taylorreihe (bezüglich
durch seine Taylorreihe (bezüglich 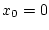 ) darstellen läßt.
Der nächste Satz liefert ein Kriterium für diese Eigenschaft:
) darstellen läßt.
Der nächste Satz liefert ein Kriterium für diese Eigenschaft:
 Als erstes stellen wir fest, das die Potenzreihe
wegen
Als erstes stellen wir fest, das die Potenzreihe
wegen
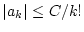 den Konvergenzradius
den Konvergenzradius 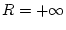 besitzt. Insbesondere konvergiert diese Reihe für alle
besitzt. Insbesondere konvergiert diese Reihe für alle
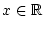 .
Zur Abschätzung des Restgliedes verwenden wir die Formel
Für
.
Zur Abschätzung des Restgliedes verwenden wir die Formel
Für 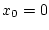 und
und 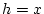 folgt
und damit
folgt
und damit
Ist eine Funktion in einer gewissen Umgebung von 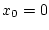 durch
ihre Taylorreihe darstellbar, so konvergiert nach der allgemeinen
Theorie der Potenzreihen die Taylorreihe im Inneren des Konvergenzkreises
mit dem Konvergenzradius
durch
ihre Taylorreihe darstellbar, so konvergiert nach der allgemeinen
Theorie der Potenzreihen die Taylorreihe im Inneren des Konvergenzkreises
mit dem Konvergenzradius 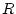 absolut, in jedem
absolut, in jedem
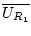 mit
mit 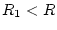 gleichmäßig und die Reihe ist in
gleichmäßig und die Reihe ist in 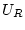 beliebig
oft gliedweise komplex differenzierbar.
beliebig
oft gliedweise komplex differenzierbar.
Man kann die oben gegebenen Betrachtungen sofort auf Taylorreihen
bezüglich eines Punktes
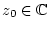 verallgemeinern.
Gilt
verallgemeinern.
Gilt 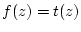 für
für
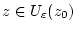 ,
,
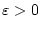 ,
so sagt man, daß die Funktion
,
so sagt man, daß die Funktion 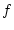 in der Umgebung
in der Umgebung
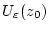 von
von 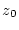 durch ihre Taylorreihe darstellbar ist.
durch ihre Taylorreihe darstellbar ist.
Zum Abschluß geben wir noch folgende Definitionen:
Definition 2.11.6.2
Es sei
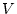
eine offene Teilmenge in
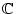
. Wir nennen
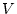
zusammenhängend, wenn zu beliebigen
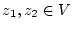
eine Jordansche Kurve endlicher Länge
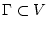
existiert,
welche
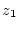
und
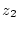
verbindet.
Definition 2.11.6.3
Es sei
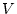
eine offene, zusammenhängende Teilmenge von
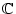
.
Ist eine Funktion
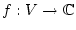
in einer gewissen Umgebung
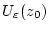
,
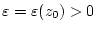
,
jedes beliebigen Punktes
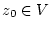
durch ihre Taylorreihe
darstellbar, so nennt man
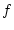
eine
analytische Funktion
in
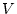
.




Next: Die Eulerschen Integrale
Up: Potenzreihen
Previous: Zur Differentation von Potenzreihen.
Contents
2003-09-05
![]() ,
, ![]() , eine im Punkt
, eine im Punkt
![]() beliebig oft reell differenzierbare Funktion. Die Taylorsche
Formel bezüglich des Punktes
beliebig oft reell differenzierbare Funktion. Die Taylorsche
Formel bezüglich des Punktes ![]() sagt aus, daß
sagt aus, daß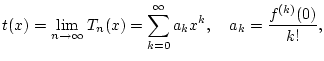
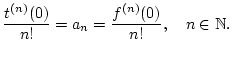
![]() und
und ![]() auf ihrem gemeinsamen Definitionsbereich
übereinstimmen. Als Beispiel betrachte man die Funktion
auf ihrem gemeinsamen Definitionsbereich
übereinstimmen. Als Beispiel betrachte man die Funktion
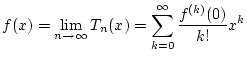
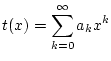
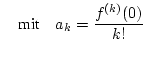
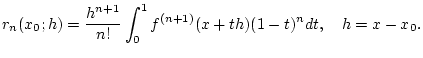
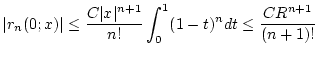
![]() durch
ihre Taylorreihe darstellbar, so konvergiert nach der allgemeinen
Theorie der Potenzreihen die Taylorreihe im Inneren des Konvergenzkreises
mit dem Konvergenzradius
durch
ihre Taylorreihe darstellbar, so konvergiert nach der allgemeinen
Theorie der Potenzreihen die Taylorreihe im Inneren des Konvergenzkreises
mit dem Konvergenzradius ![]() absolut, in jedem
absolut, in jedem
![]() mit
mit ![]() gleichmäßig und die Reihe ist in
gleichmäßig und die Reihe ist in ![]() beliebig
oft gliedweise komplex differenzierbar.
beliebig
oft gliedweise komplex differenzierbar.