Die Methode der arithmetischen Mittel nach Cesaro.

Es sei $\{a_{k}\}_{k=1}^{\infty }$ eine Folge reeller oder komplexer Zahlen. Wir betrachten die Folge der Partialsummen $S_{n}=\sum _{k=1}^{n}a_{k}$. Konvergiert die Folge der arithmetischen Mittel der Partialsummen

$$\lim _{n\to \infty }\frac{S_{1}+\ldots +S_{n}}{n}=S,$$

dann konvergiert die Reihe $\sum _{k=1}^{\infty }a_{k}$ im Sinne der arithmetischen Mittel von Cesaro und nimmt dabei den Wert $S$ an.

Aufgabe 1.9.3.1   Beweisen Sie die Regularität und die Linearität dieser Summationsmethode!

Beispiel 1.9.3.2   Es sei $a_{k}=(-1)^{k+1}$, $k\in \mathbb{N}$. Dann gilt

$$S_{1}=1,\quad S_{2}=0,\quad S_{3}=1,\quad S_{4}=0,\ldots$$

und folglich

$$\lim _{n\to \infty }\frac{S_{1}+\ldots +S_{n}}{n}=\frac{1}{2}.$$

Damit konvergiert die Reihe $\sum _{k=1}^{\infty }(-1)^{k+1}$ im Sinne der arithmetischen Mittel von Cesaro und nimmt den Wert $\frac{1}{2}$ an.

Im Vergleich mit Beispiel 1.9.2.1 sehen wir, daß die untersuchte Reihe nach Poisson-Abel und nach Cesaro den gleichen Grenzwert annimmt. Dies illustriert den folgenden Satz von Frobenius, welcher die Theorie der Summierbarkeit nach Cesaro mit der Summierbarkeit nach Poisson und Abel verbindet:

Satz 1.9.3.3   Konvergiert die Reihe $\sum _{k=1}^{\infty }a_{k}$ im Sinne der arithmetischen Mittel von Cesaro, so konvergiert diese Reihe ebenfalls nach der Potenzreihenmethode von Poisson und Abel gegen denselben Grenzwert.

Aufgabe 1.9.3.4   Untersuchen Sie, ob die Reihe $1-2+3-4+\ldots$ nach Cesaro bzw. nach Poisson-Abel konvergiert und berechnen Sie gegebenenfalls den Wert dieser Reihe.

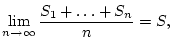
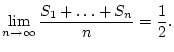
Da Cesaro-konvergente Reihen auch nach Poisson-Abel konvergieren, so läßt sich zur Überprüfung der gewöhnlichen Konvergenz natürlich der Satz von Tauber anwenden. Man kann diesen Satz aber unter der stärkeren Voraussetzung der Cesaro-Konvergenz zum Satz von Hardy verfeinern:

Satz 1.9.3.5   Konvergiert die Reihe $\sum _{k=1}^{\infty }a_{k}$ nach Cesaro gegen $A$ und gilt

$$\vert na_{n}\vert\leq C,\quad n\in \mathbb{N},$$

so konvergiert die Reihe $\sum _{k=1}^{\infty }a_{k}$ auch im üblichen Sinne gegen $A.$