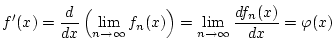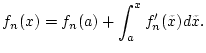Next: Die Differentation von Funktionenreihen.
Up: Zum Vertauschen von Grenzwert
Previous: Zum Vertauschen von Grenzwert
Contents
Wir erinnern, daß
![% latex2html id marker 25691
$ C^{1}([a,b],\mathbb{K}^{d}) $](img1144.png) für die Menge
der in
für die Menge
der in ![$ ]a,b[ $](img1145.png) stetig differenzierbaren Funktionen steht, die
sich zusammen mit ihrer Ableitung stetig auf
stetig differenzierbaren Funktionen steht, die
sich zusammen mit ihrer Ableitung stetig auf ![$ [a,b] $](img87.png) fortsetzen
lassen. Wir betrachten deshalb diese Ableitungen als stetige Funktion
auf dem abgeschlossenen Intervall
fortsetzen
lassen. Wir betrachten deshalb diese Ableitungen als stetige Funktion
auf dem abgeschlossenen Intervall ![$ [a,b] $](img87.png) .
.
Satz 2.6.1.1
Wir betrachten eine Funktionenfolge
![% latex2html id marker 25705
$ f_{n}\in C^{1}([a,b],\mathbb{K}^{d}) $](img1146.png) ,
,
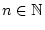 ,
so daß zum einen der Grenzwert
existiert und desweiteren der Grenzwert
angenommen wird. Dann gilt
,
so daß zum einen der Grenzwert
existiert und desweiteren der Grenzwert
angenommen wird. Dann gilt
![% latex2html id marker 25715
$ f\in C^{1}([a,b],\mathbb{K}^{d}) $](img1151.png) und
und
 Die Funktionen
Die Funktionen 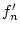 sind stetig und besitzt nach Satz 4.6.3.
des Skriptes zur Analysis I eine Stammfunktion, d.h.
Geht man hier unter Anwendung von Satz 2.5.1.1 zum Grenzwert
sind stetig und besitzt nach Satz 4.6.3.
des Skriptes zur Analysis I eine Stammfunktion, d.h.
Geht man hier unter Anwendung von Satz 2.5.1.1 zum Grenzwert
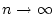 über, so gilt
über, so gilt
Nach Satz 2.3.2.1 ist 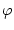 als gleichmäßiger
Grenzwert der stetigen Funktionen
als gleichmäßiger
Grenzwert der stetigen Funktionen 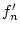 selbst stetig und
besitzt damit eine Stammfunktion, welche nach Formel (2.6.1.1)
mit
selbst stetig und
besitzt damit eine Stammfunktion, welche nach Formel (2.6.1.1)
mit 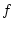 übereinstimmt. Also gilt
übereinstimmt. Also gilt
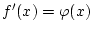 für
für
![$ x\in \, ]a,b[ $](img1160.png) und wegen der Eindeutigkeit der stetigen
Fortsetzung auch in den Randpunkten des Intervalles.
und wegen der Eindeutigkeit der stetigen
Fortsetzung auch in den Randpunkten des Intervalles.





Next: Die Differentation von Funktionenreihen.
Up: Zum Vertauschen von Grenzwert
Previous: Zum Vertauschen von Grenzwert
Contents
2003-09-05
![]() für die Menge
der in
für die Menge
der in ![]() stetig differenzierbaren Funktionen steht, die
sich zusammen mit ihrer Ableitung stetig auf
stetig differenzierbaren Funktionen steht, die
sich zusammen mit ihrer Ableitung stetig auf ![]() fortsetzen
lassen. Wir betrachten deshalb diese Ableitungen als stetige Funktion
auf dem abgeschlossenen Intervall
fortsetzen
lassen. Wir betrachten deshalb diese Ableitungen als stetige Funktion
auf dem abgeschlossenen Intervall ![]() .
.