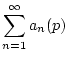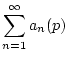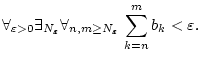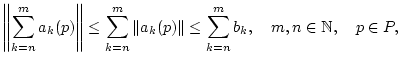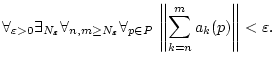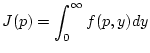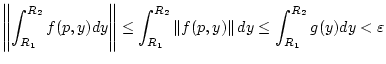Next: Potenzreihen
Up: Kriterien zur gleichmäßigen Konvergenz
Previous: Das Cauchy-Kriterium zur gleichmäßigen
Contents
Satz 2.10.4.1
Es sei
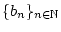 eine Folge positiver Zahlen,
für welche die Reihe
eine Folge positiver Zahlen,
für welche die Reihe
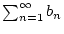 konvergiert.
Desweiteren erfülle die Funktionenfolge
konvergiert.
Desweiteren erfülle die Funktionenfolge
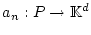 ,
,
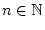 die Ungleichung
Dann konvergiert die Reihe
die Ungleichung
Dann konvergiert die Reihe
 Wenn die Reihe
Wenn die Reihe
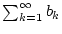 konvergiert, so gilt
nach dem Cauchy-Kriterium (1.2.1.1)
Da
so folgt
Nach Satz 2.10.2.1 konvergiert
konvergiert, so gilt
nach dem Cauchy-Kriterium (1.2.1.1)
Da
so folgt
Nach Satz 2.10.2.1 konvergiert
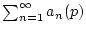 damit gleichmäßig bezüglich des Parameters
damit gleichmäßig bezüglich des Parameters 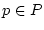 .
.

Satz 2.10.4.2
Für die Funktion
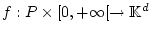 sei für alle fixierten
sei für alle fixierten 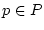 die Abbildung
die Abbildung
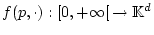 auf jedem endlichen Intervall
auf jedem endlichen Intervall ![$ [0,R] $](img1411.png) integrierbar. Desweiteren
existiere eine Funktion
integrierbar. Desweiteren
existiere eine Funktion
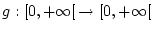 ,
so daß
Dann konvergiert das uneigentliche Integral
,
so daß
Dann konvergiert das uneigentliche Integral
 Der Satz folgt wie oben aus (1.2.1.2) und dem Cauchy-Kriterium
für gleichmäßige Konvergenz in Satz 2.10.4.2
sowie der Abschätzung
für
Der Satz folgt wie oben aus (1.2.1.2) und dem Cauchy-Kriterium
für gleichmäßige Konvergenz in Satz 2.10.4.2
sowie der Abschätzung
für
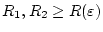 .
.

2003-09-05