



Next: Zur Stetigkeit der Grenzfunktion
Up: Das Vertauschen von Grenzwerten
Previous: Problemstellung.
Contents
WIr formulieren und beweisen jetzt den zentralen Satz dieses Kapitels.
Wir merken an, das in diesem Satz die Existenz der Grenzwerte
nicht vorausgesetzt wird, diese folgt aus der gleichmäßigen Konvergenz
von (2.2.2.1) bzw. (2.2.2.2).
 O.B.d.A. werde de Grenzwert (2.2.2.1) gleichmäßig erreicht.
O.B.d.A. werde de Grenzwert (2.2.2.1) gleichmäßig erreicht.
Schritt 1: Die Konvergenz von
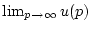 .
Nach der Dreiecksungleichung gilt
.
Nach der Dreiecksungleichung gilt
Da 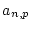 für
für
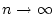 gleichmäßig bezüglich
gleichmäßig bezüglich 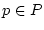 gegen
gegen 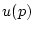 konvergiert, so gilt
konvergiert, so gilt
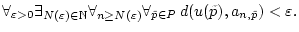 |
(2.2.2.3) |
Für vorgegebenes
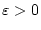 und
und
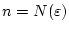 sowie
sowie
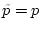 bzw.
bzw.
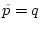 folgt insbesondere
Da nach (2.2.2.1) insbesondere die Folge
folgt insbesondere
Da nach (2.2.2.1) insbesondere die Folge
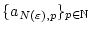 für
für
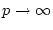 konvergiert, so ist dies eine Cauchy-Folge
und es existiert ein
konvergiert, so ist dies eine Cauchy-Folge
und es existiert ein
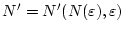 , so
daß
, so
daß
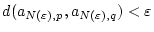 für alle
für alle
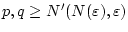 und folglich
Daraus folgt
und folglich
Daraus folgt
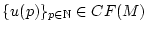 . Da
. Da 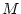 vollständig ist, so besitzt die Folge
vollständig ist, so besitzt die Folge
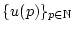 einen Grenzwert
einen Grenzwert
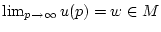 .
.
Schritt 2: Die Konvergenz von
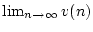 .2.2Wegen der gleichmäßigen Konvergenz von (2.2.2.1) existiert
in Übereinstimmung mit (2.2.2.3) ein
.2.2Wegen der gleichmäßigen Konvergenz von (2.2.2.1) existiert
in Übereinstimmung mit (2.2.2.3) ein
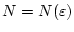 ,
so daß
,
so daß
Geht man in dieser Ungleichung zum Grenzwert
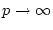 über,
so folgt aus
sowie aus der Stetigkeit der Abstandsfunktion
Damit gilt
über,
so folgt aus
sowie aus der Stetigkeit der Abstandsfunktion
Damit gilt

Aufgabe 2.2.2.2
Es seien
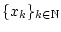
und
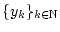
Folgen in
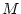
, so daß
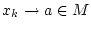
und
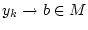
für
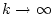
. Zeigen Sie, daß dann
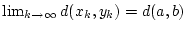
.




Next: Zur Stetigkeit der Grenzfunktion
Up: Das Vertauschen von Grenzwerten
Previous: Problemstellung.
Contents
2003-09-05
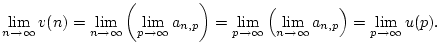
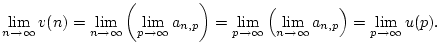
![]() O.B.d.A. werde de Grenzwert (2.2.2.1) gleichmäßig erreicht.
O.B.d.A. werde de Grenzwert (2.2.2.1) gleichmäßig erreicht.
![]() .
Nach der Dreiecksungleichung gilt
.
Nach der Dreiecksungleichung gilt
![]() .2.2Wegen der gleichmäßigen Konvergenz von (2.2.2.1) existiert
in Übereinstimmung mit (2.2.2.3) ein
.2.2Wegen der gleichmäßigen Konvergenz von (2.2.2.1) existiert
in Übereinstimmung mit (2.2.2.3) ein
![]() ,
so daß
,
so daß