



Next: Zur Stetigkeit von parameterabhängigen
Up: Das Vertauschen von Grenzwert
Previous: Zum Vertauschen des Integralzeichens
Contents
Es seien
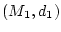 und
und
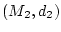 metrische Räume.
Auf dem kartesischen Produkt
metrische Räume.
Auf dem kartesischen Produkt
definieren wir die Funktion
für
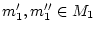 und
und
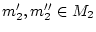 .
.
Aufgabe 2.5.4.1
Beweisen Sie, daß
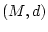
ein metrischer Raum ist.
Satz 2.5.4.2
Es seien
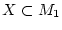 und
und
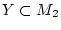 kompakte Mengen im jeweiligen metrischen Raum. Dann ist die Menge
kompakte Mengen im jeweiligen metrischen Raum. Dann ist die Menge
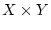 kompakt im metrischen Raum
kompakt im metrischen Raum
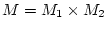 .
.
 Es sei
Es sei
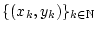 eine Folge aus
eine Folge aus
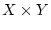 . Da
. Da 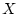 kompakt ist, so existiert eine Teilfolge
kompakt ist, so existiert eine Teilfolge
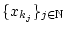 aus
aus
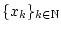 welche gegen ein Element
welche gegen ein Element
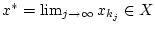 konvergiert. Desweiteren kann man wegen der Kompaktheit von
konvergiert. Desweiteren kann man wegen der Kompaktheit von 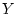 aus
aus
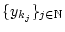 eine Teilfolge
eine Teilfolge
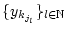 auswählen, welche gegen
auswählen, welche gegen
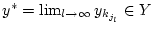 konvergiert. Da dann
konvergiert. Da dann
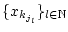 wiederum
eine Teilfolge von
wiederum
eine Teilfolge von
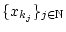 ist, so
gilt auch
ist, so
gilt auch
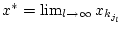 . Wegen
konvergiert damit die Teilfolge
. Wegen
konvergiert damit die Teilfolge
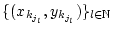 von
von
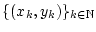 in
in
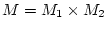 gegen
gegen
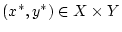 . Also ist
. Also ist 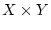 kompakt.
kompakt.

2003-09-05
![]() und
und
![]() metrische Räume.
Auf dem kartesischen Produkt
metrische Räume.
Auf dem kartesischen Produkt