



Next: Die Integration parameterabhängiger Integrale.
Up: Differenzieren und Integrieren von
Previous: Differenzieren und Integrieren von
Contents
Es sei
![$ \Omega =[a,b]\times [c,d] $](img1190.png) . Wir betrachten eine Funktion
. Wir betrachten eine Funktion
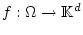 und setzen
und setzen
Wir wollen untersuchen, unterwelchen Bedingungen die Funktion
![% latex2html id marker 25897
$ J:[a,b]\to \mathbb{K}^{d} $](img1193.png) differenzierbar ist.
differenzierbar ist.
 Schritt 1: Wir betrachten zunächst reellwertige Funktionen.
Wegen
Schritt 1: Wir betrachten zunächst reellwertige Funktionen.
Wegen
![% latex2html id marker 25930
$ f(x,\cdot )\in C([c,d],\mathbb{R}) $](img1201.png) ist das Integral
für alle
ist das Integral
für alle
![$ x\in [a,b] $](img1194.png) wohldefiniert. Für
wohldefiniert. Für
![$ x\in ]a,b[ $](img1173.png) und
genügend kleine
und
genügend kleine 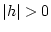 mit
mit
![$ x+h\in [a,b] $](img1204.png) gilt
gilt
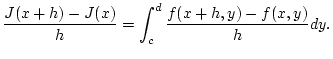 |
(2.7.1.1) |
Schritt 2: Wir zeigen nun, daß unter den Voraussetzungen des
Satzes für fixiertes
![$ x=x^{*}\in ]a,b[ $](img1206.png) der Grenzwert
der Grenzwert
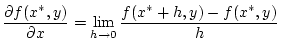 ![% latex2html id marker 25951
$\displaystyle \mbox {gleichm.\, bezgl.}\, y\in [c,d]$](img1208.png) |
(2.7.1.2) |
angenommen wird. Tatsächlich, nach der Formel von Lagrange ist
für geeignetes
![$ t_{y}\in [0,1] $](img1210.png) und damit auch
Als stetige Funktion auf der kompakten Menge
und damit auch
Als stetige Funktion auf der kompakten Menge
![$ \Omega =[a,b]\times [c,d] $](img1190.png) ist
ist
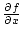 gleichmäßig stetig. Dann
existiert für jedes
gleichmäßig stetig. Dann
existiert für jedes
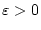 ein
ein
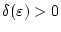 ,
so daß
Dies impliziert (2.7.1.2).
,
so daß
Dies impliziert (2.7.1.2).
Schritt 3: Wir können damit in (2.7.1.1)
für 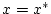 zum Grenzwert
zum Grenzwert 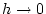 übergehen und nach
Satz 2.5.3.1 auf der rechten Seite der Gleichung das
Integralzeichen mit dem Grenzwert vertauschen
übergehen und nach
Satz 2.5.3.1 auf der rechten Seite der Gleichung das
Integralzeichen mit dem Grenzwert vertauschen
Man kann nun leicht durch komponentweise Anwendung die für reelle
Funktionen bewiesene Aussage auf Funktionen mit Werten in
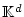 ausdehnen.
ausdehnen.





Next: Die Integration parameterabhängiger Integrale.
Up: Differenzieren und Integrieren von
Previous: Differenzieren und Integrieren von
Contents
2003-09-05
![]() . Wir betrachten eine Funktion
. Wir betrachten eine Funktion
![]() und setzen
und setzen
![$\displaystyle J(x)=\int _{c}^{d}f(x,y)dy,\quad x\in [a,b].$](img1192.png)
![$\displaystyle \frac{dJ(x)}{dx}=\int _{c}^{d}\frac{\partial f(x,y)}{\partial x}dy,\quad x\in [a,b].$](img1200.png)
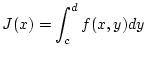
![]() der Grenzwert
der Grenzwert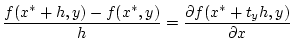
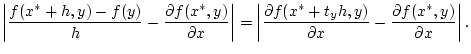
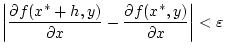
![]() zum Grenzwert
zum Grenzwert ![]() übergehen und nach
Satz 2.5.3.1 auf der rechten Seite der Gleichung das
Integralzeichen mit dem Grenzwert vertauschen
übergehen und nach
Satz 2.5.3.1 auf der rechten Seite der Gleichung das
Integralzeichen mit dem Grenzwert vertauschen
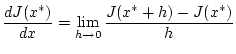
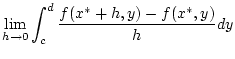
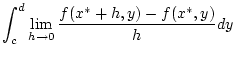
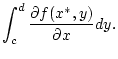
![]() ausdehnen.
ausdehnen.
![]()