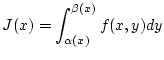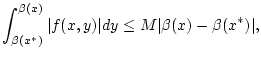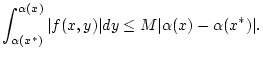Next: Zur Differenzierbarkeit.
Up: Stetigkeit und Differenzierbarkeit von
Previous: Zur Formulierung des Problems.
Contents
Satz 2.8.2.1
Es gelte
Dann ist die Funktion
stetig in allen Punkten
![$ x\in [a,b] $](img1194.png) .
.
 Wir fixieren einen Punkt
Wir fixieren einen Punkt
![$ x^{*}\in [a,b] $](img1266.png) und setzen
und setzen
![$\displaystyle J(x)=J_{0}(x)+J_{+}(x)-J_{-}(x),\quad x\in [a,b],$](img1267.png) |
(2.8.2.1) |
mit
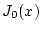 |
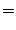 |
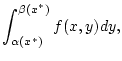 |
(2.8.2.2) |
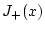 |
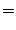 |
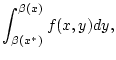 |
(2.8.2.3) |
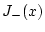 |
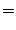 |
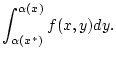 |
(2.8.2.4) |
Nach Satz 2.5.5.1 ist wegen
![% latex2html id marker 26218
$ f\in C([a,b]\times [\alpha (x^{*}),\beta (x^{*})],\mathbb{R}) $](img1274.png) das Integral
das Integral 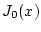 in allen Punkten
in allen Punkten
![$ x\in [a,b] $](img1194.png) stetig
und folglich
Desweiteren ist
stetig
und folglich
Desweiteren ist 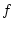 als stetige Funktion auf der kompakten Menge
als stetige Funktion auf der kompakten Menge
![$ [a,b]\times [c,d] $](img1198.png) beschränkt, d.h.
Daraus folgt
beschränkt, d.h.
Daraus folgt
Da die Abbildungen 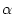 und
und 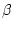 insbesondere im
Punkt
insbesondere im
Punkt 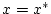 stetig sind, so folgt
stetig sind, so folgt
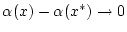 und
und
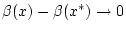 für
für
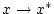 und
damit
Dies ergibt
und
damit
Dies ergibt





Next: Zur Differenzierbarkeit.
Up: Stetigkeit und Differenzierbarkeit von
Previous: Zur Formulierung des Problems.
Contents
2003-09-05