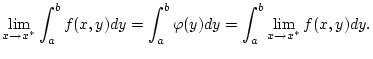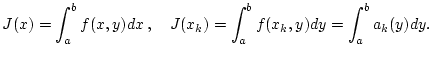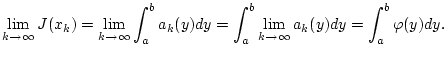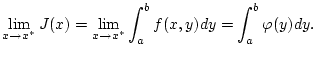Next: Das kartesische Produkt metrischer
Up: Das Vertauschen von Grenzwert
Previous: Zur Integration von Funktionenreihen.
Contents
Es sei 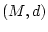 ein metrischer Raum,
ein metrischer Raum,
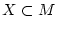 und
und
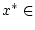
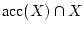 .
.
Satz 2.5.3.1
Es sei
![% latex2html id marker 25481
$ f:X\times [a,b]\to \mathbb{K}^{d} $](img1092.png) eine Abbildung, so daß für jedes
eine Abbildung, so daß für jedes 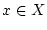 die Abbildung
die Abbildung
![% latex2html id marker 25485
$ f(x,\cdot ):[a,b]\to \mathbb{K}^{d} $](img1093.png) auf
auf ![$ [a,b] $](img87.png) Riemann-integrierbar ist. Desweiteren werde der Grenzwert
angenommen. Dann ist
Riemann-integrierbar ist. Desweiteren werde der Grenzwert
angenommen. Dann ist 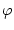 auf
auf ![$ [a,b] $](img87.png) Riemann-integrierbar
und es existiert der Grenzwert
Riemann-integrierbar
und es existiert der Grenzwert
 Es sei
Es sei
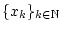 eine Folge von Gliedern
eine Folge von Gliedern
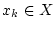 ,
,
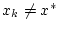 , mit der Eigenschaft
, mit der Eigenschaft
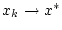 für
für
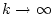 . Wir setzen
Nach Aufgabe 2.1.5.2 konvergiert
. Wir setzen
Nach Aufgabe 2.1.5.2 konvergiert 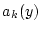 gleichmäßig
bezüglich
gleichmäßig
bezüglich
![$ y\in [a,b] $](img1101.png) gegen
gegen
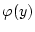 . Wir setzen
Nach Satz 2.5.1.1 gilt
Da die rechte Seite nicht von der konkreten Wahl der Folge
. Wir setzen
Nach Satz 2.5.1.1 gilt
Da die rechte Seite nicht von der konkreten Wahl der Folge
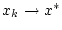 abhängt, so folgt
abhängt, so folgt

2003-09-05
![]() ein metrischer Raum,
ein metrischer Raum,
![]() und
und
![]()
![]() .
.