



Next: Das Cauchy-Kriterium zur gleichmäßigen
Up: Kriterien zur gleichmäßigen Konvergenz
Previous: Kriterien zur gleichmäßigen Konvergenz
Contents
 Angenommen (2.10.1.2) gilt. Dann folgt für jedes fixierte
Angenommen (2.10.1.2) gilt. Dann folgt für jedes fixierte
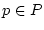 auch
auch
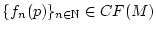 .
Da
.
Da 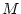 vollständig ist, so existieren punktweise die Grenzwerte
Geht man in der Ungleichung
zum Grenzwert
über, so folgt zudem die Gleichmäßigkeit in (2.10.1.1).
vollständig ist, so existieren punktweise die Grenzwerte
Geht man in der Ungleichung
zum Grenzwert
über, so folgt zudem die Gleichmäßigkeit in (2.10.1.1).
Umgekehrt bedeutet (2.10.1.1)
und damit
für alle
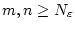 .
.

2003-09-05