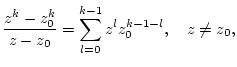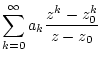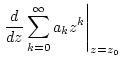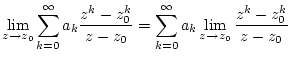Next: Die Taylorreihe.
Up: Potenzreihen
Previous: Zur Differentation von Potenzreihen.
Contents
Bei der Untersuchung der Differenzierbarkeit von Funktionenreihen
haben wir uns der Einfachheit halber in Kapitel 2.6
auf reelle Differenzierbarkeit beschränkt und in den Beweisen auch
Methoden der reellen Ableitungen eingesetzt2.5. Andererseits lassen sich die oben gesammelten Beobachtung zur reellen
Differenzierbarkeit von Potenzreihen auch auf komplexe Differenzierbarkeit
ausweiten:
 Es sei
Es sei
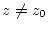 ,
,
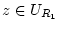 ,
,
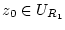 sowie
sowie
![$ R_{1}\in \, ]\vert z_{0}\vert,R[\, $](img1500.png) . Dann gilt
und damit
. Dann gilt
und damit
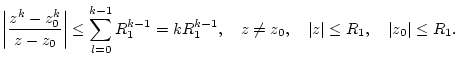 |
(2.11.5.2) |
Da nach Lemma 2.11.4.1 die Potenzreihe
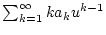 auch den Konvergenzradius
auch den Konvergenzradius 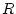 besitzt, so ist nach Korollar 2.11.3.2
die Reihe
besitzt, so ist nach Korollar 2.11.3.2
die Reihe
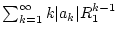 konvergent.
Daraus folgt zusammen mit (2.11.5.2) nach
dem Majorantenkriterium von Weierstrass, daß die Reihe
gleichmäßig bezüglich
konvergent.
Daraus folgt zusammen mit (2.11.5.2) nach
dem Majorantenkriterium von Weierstrass, daß die Reihe
gleichmäßig bezüglich
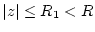 konvergiert. Nach Satz
2.3.4.1 folgt für
konvergiert. Nach Satz
2.3.4.1 folgt für
 dann
dann





Next: Die Taylorreihe.
Up: Potenzreihen
Previous: Zur Differentation von Potenzreihen.
Contents
2003-09-05