



Next: Zum Beweis von Satz
Up: Der Satz von Weierstrass
Previous: Der Satz von Weierstrass
Contents
Der folgende Satz diskutiert, inwieweit man stetige Funtionen auf
einem beschränkten Intervall gleichmäßig durch Polynome approximieren
kann.
Satz 2.13.1.1
Es sei
![% latex2html id marker 28030
$ f\in C([a,b],\mathbb{C}) $](img1667.png) . Dann
existiert eine Folge von Polynomen
. Dann
existiert eine Folge von Polynomen 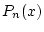 , so daß
, so daß
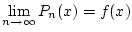 ![% latex2html id marker 28037
$\displaystyle \quad \mbox {gleichmäßig\, bezüglich}\quad x\in [a,b].$](img1670.png) |
(2.13.1.1) |
Wir haben bereits im Abschnitt 2.3.3 in
Zusammenhang mit Satz 2.1.3.1 diskutiert, das hier
gleichmäßige Konvergenz der Konvergenz im Funktionenraum
![% latex2html id marker 28040
$ C([a,b],\mathbb{C}) $](img1671.png) entspricht. Insbesondere ist (2.13.1.1) wegen Satz
2.1.3.1 (unter Anwendung des Satzes von Weierstraß
über stetige Funktionen auf kompakten Mengen) gleichbedeutend zu
entspricht. Insbesondere ist (2.13.1.1) wegen Satz
2.1.3.1 (unter Anwendung des Satzes von Weierstraß
über stetige Funktionen auf kompakten Mengen) gleichbedeutend zu
d.h. 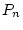 konvergiert im Raum
konvergiert im Raum
![% latex2html id marker 28055
$ C([a,b],\mathbb{C}) $](img1676.png) gegen
gegen 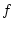 .
.
Es sei
![% latex2html id marker 28059
$ \Omega \subset C([a,b],\mathbb{C}) $](img1677.png) die Menge aller
Polynome mit komplexen Koeffizienten auf dem Intervall
die Menge aller
Polynome mit komplexen Koeffizienten auf dem Intervall ![$ [a,b] $](img87.png) .
Dann ist Satz 2.13.1.1 gleichbedeutend damit, daß für
jedes
.
Dann ist Satz 2.13.1.1 gleichbedeutend damit, daß für
jedes
![% latex2html id marker 28063
$ f\in C([a,b],\mathbb{C}) $](img1678.png) eine Folge von
eine Folge von
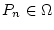 existiert, welche gegen
existiert, welche gegen 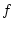 in der Metrik von
in der Metrik von
![% latex2html id marker 28069
$ C([a,b],\mathbb{C}) $](img1680.png) konvergiert. Damit gilt entweder
konvergiert. Damit gilt entweder
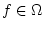 oder
oder
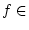
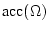 ,
d.h.
,
d.h.
Mit anderen Worten (vergleiche Abschnitt 2.12.9 im Skript Analysis
1) ist Satz 2.13.1.1 äquivalent zu
Satz 2.13.1.2
Die Menge der Polynome 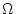 ist dicht in
ist dicht in
![% latex2html id marker 28087
$ C([a,b],\mathbb{C}) $](img1687.png) .
.




Next: Zum Beweis von Satz
Up: Der Satz von Weierstrass
Previous: Der Satz von Weierstrass
Contents
2003-09-05
![]() die Menge aller
Polynome mit komplexen Koeffizienten auf dem Intervall
die Menge aller
Polynome mit komplexen Koeffizienten auf dem Intervall ![]() .
Dann ist Satz 2.13.1.1 gleichbedeutend damit, daß für
jedes
.
Dann ist Satz 2.13.1.1 gleichbedeutend damit, daß für
jedes
![]() eine Folge von
eine Folge von
![]() existiert, welche gegen
existiert, welche gegen ![]() in der Metrik von
in der Metrik von
![]() konvergiert. Damit gilt entweder
konvergiert. Damit gilt entweder
![]() oder
oder
![]()
![]() ,
d.h.
,
d.h.