Next:
Grundlegende Definitionen
Up:
Analysis 2
Previous:
Contents
Contents
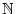Reihen und uneigentliche Integrale
Subsections
Grundlegende Definitionen
Reihen über
und uneigentlich Integrale auf
.
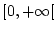Reihen über
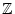und uneigentliche Integrale auf
.
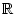Einige Beispiele.
Uneigentliche Integrale auf endlichem Integrationsbereich.
Der Cauchysche Hauptwert.
Wichtige Eigenschaften von Reihen und uneigentlichen Integralen
Das Cauchy-Kriterium.
Eine hinreichende Bedingung.
Die Linearität von Reihen und uneigentlichen Integralen.
Der Umordnungssatz. Summierung über allgemeine Indexmengen. Doppelreihen.
Die Monotonität.
Der Umordnungssatz.
Der Riemannsche Umordnungssatz.
Allgemeine Reihen mit nichtnegativen Gliedern
Wichtige Eigenschaften von verallgemeinerten Reihen mit nichtnegativen Gliedern.
Doppelreihen.
Multiplikation von Reihen mit nichtnegativen Gliedern.
Konvergenzkriterien für Reihen nichtnegativer Glieder und für uneigentliche Integrale nichtnegativer Funktionen
Das Vergleichskriterium.
Das Wurzelkriterium von Cauchy.
Das Quotientenkriterium von d'Alambert.
Das Integralkriterium von Cauchy.
Es gibt keine universelle Vergleichsfunktion.
Das Raabsche Kriterium
Das Kummersche Kriterium.
Konvergenzkriterien für Reihen mit nichtnegativen Gliedern in Limesform .
Der obere und der untere Grenzwert.
Das Vergleichskriterium in Limesform.
Das Wurzelkriterium in Limesform.
Das Quotientenkriterium in Limesform.
Absolute und bedingte Konvergenz
Definitionen.
Zum Zusammenhang zwischen absoluter und bedingter Konvergenz.
Weitere elementare Kriterien für absolute Konvergenz.
Der Umordnungssatz für absolut konvergente Reihen.
Konvergenzkriterien für im Allgemeinen nicht absolut konvergente Folgen
Die Abelsche partielle Summation.
Das Abelsche Kriterium.
Das Kriterium von Dirichlet.
Das Leibniz-Kriterium für alternierende Reihen
Das Kriterium von Dirichlet für uneigentliche Integrale.
Unendliche Produkte
Definition.
Zusammenhang zwischen Reihen und unendlichen Produkten.
Die Summierung divergenter Reihen
Verallgemeinerte Summationsmethoden.
Die Potenzreihenmethode von Poisson und Abel.
Die Methode der arithmetischen Mittel nach Cesaro.
2003-09-05
und uneigentlich Integrale
auf
.
und uneigentliche
Integrale auf
.