Next: Es gibt keine universelle
Up: Konvergenzkriterien für Reihen nichtnegativer
Previous: Das Quotientenkriterium von d'Alambert.
Contents
Wir haben bereits angemerkt, daß man Reihen als Spezialfälle von uneigentlichen
Integralen auffassen kann. Dann ist es aber auch möglich, aus der
Konvergenz gewisser Integrale auf die Konvergenz bestimmter Reihen
zu schließen.
Satz 1.4.4.1
Es sei
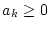 für
für
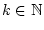 . Die Funktion
. Die Funktion
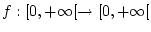 sei monoton fallend und es gelte
Dann konvergiert das uneigentliche Integral
sei monoton fallend und es gelte
Dann konvergiert das uneigentliche Integral
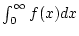 genau dann, wenn auch die Reihe
genau dann, wenn auch die Reihe
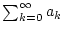 konvergiert. Dabei gilt
konvergiert. Dabei gilt
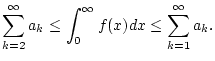 |
(1.4.4.1) |
 Als monotone Funktion ist
Als monotone Funktion ist 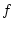 auf jedem endlichen Intervall
auf jedem endlichen Intervall ![$ [0,c] $](img149.png) integrierbar. Es sei
integrierbar. Es sei
Dann gilt
und damit nach die charakteristische Funktion des Intervalles 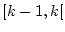 ,
,
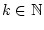 . Wegen
so konvergieren nach Satz 1.4.1.1 und 1.4.1.2
die Reihe
. Wegen
so konvergieren nach Satz 1.4.1.1 und 1.4.1.2
die Reihe
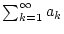 und das uneigentliche
Integral
und das uneigentliche
Integral
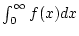 gleichzeitig und es gilt
(1.4.4.1).
gleichzeitig und es gilt
(1.4.4.1).

Mit Hilfe der Ungleichung (1.4.4.1) kann man
den numerischen Wert von Reihen durch den numerischen Wert von uneigentlichen
Integralen abschätzen. Dabei ist es oft nützlich, eine endliche Anzahl
von Summanden direkt aufzusummieren und dann (1.4.4.1)
auf den verbleibenden Rest der Reihe anzuwenden.
Beispiel 1.4.4.2
Die
harmonische Reihe
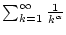
konvergiert für
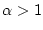
und divergiert für
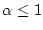
,
da daß uneigentliche Integral
für
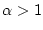
konvergiert und für
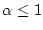
divergiert.
Aufgabe 1.4.4.3
Schätzen Sie mit Hilfe von (
1.4.4.1) die Summe
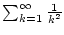
bis auf eine Genauigkeit
von
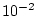
ab!
Beispiel 1.4.4.4
Wir untersuchen die Reihe
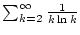
auf Konvergenz. Die Analysis der entsprechenden Integrals
zeigt, daß diese Reihe divergiert.
Betrachtet man hingegen das modifizierte Problem
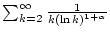 mit
mit
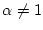 , so führt die entsprechende Rechnung auf
, so führt die entsprechende Rechnung auf
Letzterer Ausdruck konvergiert für
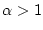
und divergiert
für
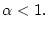
Gleiches gilt damit auch für die Reihe
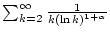
.
Aufgabe 1.4.4.5
Für welche
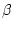
konvergiert die Reihe
Aufgabe 1.4.4.6
Es sei
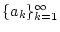
eine monotone Folge positiver
Zahlen und die Reihe
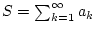
konvergiere.
Beweisen Sie, daß dann
gilt.




Next: Es gibt keine universelle
Up: Konvergenzkriterien für Reihen nichtnegativer
Previous: Das Quotientenkriterium von d'Alambert.
Contents
2003-09-05
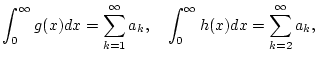
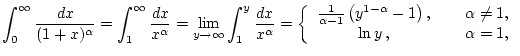
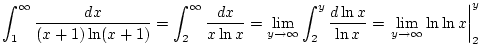
![]() mit
mit
![]() , so führt die entsprechende Rechnung auf
, so führt die entsprechende Rechnung auf