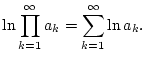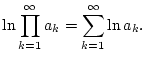Next: Die Summierung divergenter Reihen
Up: Unendliche Produkte
Previous: Definition.
Contents
Aufgrund der Stetigkeit der Logarithmus-Funktion besteht folgender
offensichtlicher Zusammenhang zwischen Reihen und unendlichen Produkten:
Satz 1.8.2.1
Es sei
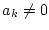 für alle
für alle
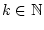 . Das unendliche
Produkt
. Das unendliche
Produkt
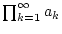 konvergiert genau dann,
wenn die Reihe
konvergiert genau dann,
wenn die Reihe
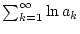 gegen einen endlichen
Wert konvergiert. Dabei gilt
gegen einen endlichen
Wert konvergiert. Dabei gilt
Aus diesem Satz folgt wegen Satz 1.2.1.3 sofort
folgende notwendige Bedingung für die Konvergenz unendlicher Produkte:
Satz 1.8.2.2
Es sei
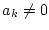 für alle
für alle
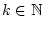 . Falls
das unendliche Produkt
. Falls
das unendliche Produkt
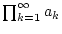 konvergiert,
so gilt
konvergiert,
so gilt
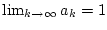 .
.
Die Untersuchung unendlicher Produkte kann damit auf die Untersuchung
von Reihen zurückgeführt werden.
2003-09-05