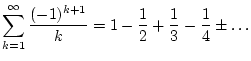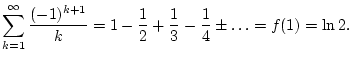Zum Zusammenhang zwischen absoluter und bedingter Konvergenz.

Satz 1.6.2.1   Konvergiert die Reihe $\sum _{k=1}^{\infty }a_{k}$ absolut, so konvergiert diese Reihe auch bedingt.

Konvergiert das uneigentliche Integral $\int _{0}^{\infty }f(x)dx$ absolut, so konvergiert $\int _{0}^{\infty }f(x)dx$ auch bedingt.

$\blacktriangleright$ Wir beweisen die Aussage im Fall der Reihe und verwenden das Cauchy-Kriterium (1.2.1.1). Aus der Dreiecksungleichung folgt

$$\left\Vert \sum _{k=m+1}^{n}a_{k}\right\Vert \leq \sum _{k=m+1}^{... ...k}\parallel =\left\Vert \sum _{k=m+1}^{n}\parallel a_{k}\parallel \right\Vert .$$ (1.6.2.1)

Konvergiert $\sum _{k=1}^{\infty }a_{k}$ absolut, d.h. konvergiert $\sum _{k=1}^{\infty }\parallel a_{k}\parallel$, dann wird die rechte Seite von (1.6.2.1) nach (1.2.1.1) kleiner als jedes vorgegebene $\varepsilon >0$ für $m\geq n\geq N_{\varepsilon }$. Gleiches gilt damit für die linke Seite der Ungleichung, woraus wiederum nach dem Cauchy-Kriterium die bedingte Konvergenz folgt. $\blacktriangleleft$

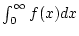
Aufgabe 1.6.2.2   Führen Sie den Beweis für das uneigentliche Integral $\int _{0}^{\infty }f(x)dx$. Erstreckt sich der Satz auch auf alle anderen Typen unbestimmter Integrale?

 

Aufgabe 1.6.2.3   Beweisen Sie, daß die Reihe

$$\sum _{k=1}^{\infty }\frac{{(-1)^{k+1}}}{k}=1-\frac{{1}}{2}+\frac{{1}}{3}-\frac{{1}}{4}\pm \ldots$$

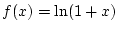
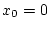
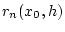
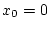
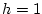
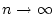
bedingt, aber nicht absolut konvergiert. Analysieren Sie die Taylorreihe für die Funktion $f(x)=\ln (1+x)$ im Punkt $x_{0}=0$ und zeigen Sie, daß der Restterm $r_{n}(x_{0},h)$ d ieser Reihe für $x_{0}=0$, $h=1$ und $n\to \infty$ verschwindet. Schließen Sie daraus, daß

$$\sum _{k=1}^{\infty }\frac{{(-1)^{k+1}}}{k}=1-\frac{{1}}{2}+\frac{{1}}{3}-\frac{{1}}{4}\pm \ldots =f(1)=\ln 2.$$

Warum genügt es i.A. nicht, im letzten Schritt nur die Konvergenz der Taylorreihe festzustellen?