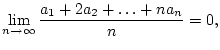Die Potenzreihenmethode von Poisson und Abel.

Es sei $\{a_{k}\}_{k=1}^{\infty }$ eine Folge reeller oder komplexer Zahlen. Dieser ordnet man die Potenzreihe $\sum _{k=1}^{\infty }a_{k}x^{k-1}$ zu. Konvergiert diese Potenzreihe für $0<x<1$ (im üblichen Sinne) bedingt gegen einen Wert

$$p(x):=\sum _{k=1}^{\infty }a_{k}x^{k-1},\quad 0<x<1,$$

und besitzt $p(x)$ den linksseitigen Grenzwert

$$A=\lim _{x\to 1-0}p(x)=\lim _{x\to 1-0}\sum _{k=1}^{\infty }a_{k}x^{k-1},$$

so konvergiert die Reihe $\sum _{k=1}^{\infty }a_{k}$ im Sinne von Poisson und Abel und nimmt dabei den Wert $A$ an.

Beispiel 1.9.2.1   Es sei $a_{k}=(-1)^{k+1}$, $k\in \mathbb{N}$. Dann konvergiert die geometrische Reihe

$$p(x)=\sum _{k=1}^{\infty }(-1)^{k+1}x^{k-1}=\frac{1}{1+x},\quad 0<x<1,$$

und $p(x)=(1+x)^{-1}$ besitzt für $x\to 1-0$ den linksseitigen Grenzwert

$$A=\lim _{x\to 1-0}p(x)=\lim _{x\to 1-0}\frac{1}{1+x}=\frac{1}{2}.$$

Damit konvergiert die Reihe

$$\sum _{k=1}^{\infty }(-1)^{k+1}=1-1+1\mp \dots$$

im Sinne von Poisson und Abel gegen den Wert $A=\frac{1}{2}$.

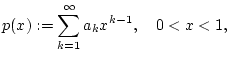
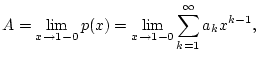
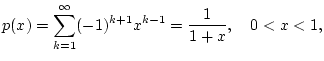
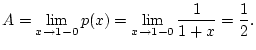
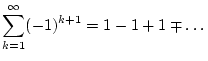
Die Linearität dieser Definition ist offensichtlich. Der folgende Satz von Abel, welchen wir ohne Beweis angeben, sichert die Regularität dieser Summationsmethode.

Satz 1.9.2.2   Konvergiert die Reihe $\sum _{k=1}^{\infty }a_{k}$ bedingt, so konvergieren die Reihen

$$p(x):=\sum _{k=1}^{\infty }a_{k}x^{k-1},$$$$\quad \mbox {für}\quad 0<x<1$$

bedingt und es gilt

$$\lim _{x\to 1-0}p(x)=\lim _{x\to 1-0}\sum _{k=1}^{\infty }a_{k}x^{k-1}=\sum _{k=1}^{\infty }a_{k}.$$

Umgekehrt folgt aus der Existenz des linksseitigen Grenzwertes

$$\lim _{x\to 1-0}\sum _{k=1}^{\infty }a_{k}x^{k-1}=A$$

im Allgemeinen nicht die Konvergenz der Reihe $\sum _{k=1}^{\infty }a_{k}$ im üblichen Sinne.

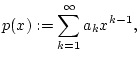
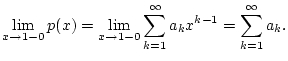
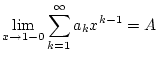
Wir formulieren an dieser Stelle noch den Satz von Tauber, welcher ein hinreichendes Kriterium dafür liefert, wann eine nach Poisson und Abel konvergente Reihe auch im üblichen Sinne konvergiert:

Satz 1.9.2.3   Die Reihen $p(x)=\sum _{k=1}^{\infty }a_{k}x^{k-1}$ seien für $0<x<1$ bedingt konvergent und es existiere der linksseitige Grenzwert

$$\lim _{x\to 1-0}p(x)=A.$$

Gilt zudem

$$\lim _{n\to \infty }\frac{{a_{1}+2a_{2}+\ldots +na_{n}}}{n}=0,$$

dann konvergiert die Reihe $\sum _{k=1}^{\infty }a_{k}=A$ auch im üblichen Sinne.