Das Quotientenkriterium in Limesform.

Satz 1.5.4.1   Es sei $a_{k}>0$ für $k\in \mathbb{N}$. Gilt $\limsup _{k\to \infty }\frac{a_{k+1}}{a_{k}}<1$, dann konvergiert die Reihe $\sum _{k=1}^{\infty }a_{k}$. Gilt hingegen $\liminf _{k\to \infty }\frac{a_{k+1}}{a_{k}}>1$, dann divergiert die Reihe $\sum _{k=1}^{\infty }a_{k}$.

$\blacktriangleright$ Falls $s=\limsup _{k\to \infty }\frac{a_{k+1}}{a_{k}}<1$, dann gilt $\frac{a_{k+1}}{a_{k}}<r$ für $s<r<1$ und $k\geq N_{r,s}$. Die erste Aussage folgt damit aus Satz 1.4.3.1. Falls $s=\liminf _{k\to \infty }\frac{a_{k+1}}{a_{k}}>1$, so gilt $\frac{a_{k+1}}{a_{k}}>r$ für $1<r<s$ und $k\geq N_{r,s}$, damit ist der Fall der Divergenz auf Satz 1.4.3.1 zurückgeführt. $\blacktriangleleft$

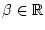
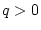
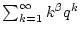
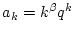
Beispiel 1.5.4.2   Es sei $\beta \in \mathbb{R}$ und $q>0$. Wir untersuchen die Reihe $\sum _{k=1}^{\infty }k^{\beta }q^{k}$ auf Konvergenz. Für $a_{k}=k^{\beta }q^{k}$ folgt

$$a_{k}^{1/k}=qk^{\beta /k}\to q$$$$\quad \mbox {für}\quad k\to \infty .$$

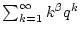
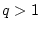
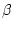
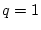
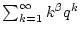
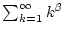
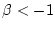
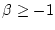
Nach dem Wurzelkriterium konvergiert $\sum _{k=1}^{\infty }k^{\beta }q^{k}$ für $q\in ]0,1[$ und divergiert für $q>1$ unabhängig vom Wert von $\beta$. Für $q=1$ liefert das Wurzelkriterium keine Antwort. Die Reihe $\sum _{k=1}^{\infty }k^{\beta }q^{k}$ geht dann in die harmonische Reihe $\sum _{k=1}^{\infty }k^{\beta }$ über, welche für $\beta <-1$ konvergiert und für $\beta \geq -1$ divergiert.