



Next: Die Monotonität.
Up: Reihen und uneigentliche Integrale
Previous: Die Linearität von Reihen
Contents
Wir betrachten in diesem Punkt Reihen, welche aus Folgen nichtnegativer
Zahlen
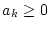 gebildet werden. Dann ist die Folge der
Partialsummen
gebildet werden. Dann ist die Folge der
Partialsummen
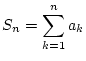 |
(1.3.0.1) |
eine monoton wachsende Folge. Diese konvergiert damit entweder
gegen eine reelle Zahl oder divergiert bestimmt gegen 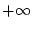 .
.
Subsections
2003-09-05
![]() gebildet werden. Dann ist die Folge der
Partialsummen
gebildet werden. Dann ist die Folge der
Partialsummen