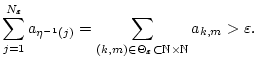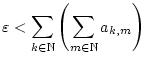Next: Multiplikation von Reihen mit
Up: Der Umordnungssatz. Summierung über
Previous: Wichtige Eigenschaften von verallgemeinerten
Contents
Eine wichtige Anwendung von verallgemeinerten Reihen sind die sogennanten
Doppelreihen. Sind 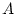 und
und 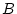 abzählbare Mengen, so ist
auch das kartesische Produkt
abzählbare Mengen, so ist
auch das kartesische Produkt 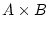 abzählbar. Damit ist
für
abzählbar. Damit ist
für
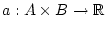 und
und
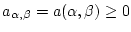 ,
,
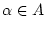 ,
,
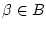 , die Reihe
, die Reihe
wohldefiniert. Insbesondere kann man mit
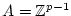 und
und
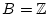 iterativ Reihen über das Gitter
iterativ Reihen über das Gitter
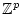 definieren.
definieren.
Eine Modifikation dieser Idee führt zu einer wichtigen Verallgemeinerung
von Satz 1.3.5. Dazu betrachten wir eine abzählbare
Familie abzählbarer Mengen
welche paarweise disjunkt sind
Wir setzen
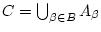 . 1.1Es sei
. 1.1Es sei
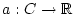 mit
mit
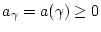 für
für
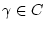 . Dann gilt:
. Dann gilt:
Satz 1.3.6.1
Die Reihe
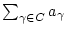 konvergiert genau dann, wenn die Reihe
konvergiert genau dann, wenn die Reihe
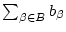 mit
mit
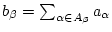 konvergiert.
Dabei gilt
konvergiert.
Dabei gilt
Führen Sie mit Hilfe bijektiver Abbildungen
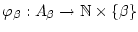 sowie
sowie
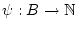 den Beweis von Satz 1.3.6.1
auf folgende Aussage zurück:
den Beweis von Satz 1.3.6.1
auf folgende Aussage zurück:
Satz 1.3.6.2
Es sei
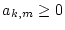 für
für
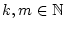 .
Dann konvergieren die Reihen in der folgenden Identität gleichzeitig
und es gilt
.
Dann konvergieren die Reihen in der folgenden Identität gleichzeitig
und es gilt
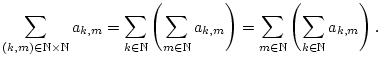 |
(1.3.6.1) |
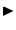 Wit nehmen zunächst an, daß die Reihe
Wit nehmen zunächst an, daß die Reihe
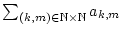 konvergiert. Wegen
konvergiert. Wegen
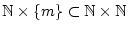 konvergiert nach Satz 1.3.5.2 jede der Reihen
konvergiert nach Satz 1.3.5.2 jede der Reihen
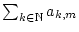 . Da außerdem
so folgt mit Hilfe der vollständigen Induktion aus Satz 1.3.5
sowie nach Satz 1.3.5.2 desweiteren
Folglich konvergiert die Reihe auf der linken Seite und es gilt
. Da außerdem
so folgt mit Hilfe der vollständigen Induktion aus Satz 1.3.5
sowie nach Satz 1.3.5.2 desweiteren
Folglich konvergiert die Reihe auf der linken Seite und es gilt
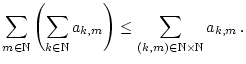 |
(1.3.6.2) |
Nach der Definition der Konvergenz verallgemeinerter Reihen gilt
für eine Bijektion
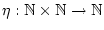 .
Für jedes
.
Für jedes
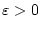 existiert damit ein
existiert damit ein
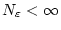 ,
so daß
Hier ist
,
so daß
Hier ist
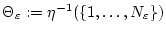 eine endliche Menge. Es sei weiterhin
eine endliche Menge. Es sei weiterhin
Wegen
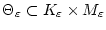 gilt für die (endlichen) Summen
gilt für die (endlichen) Summen
Im Grenzwert
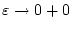 folgt
folgt
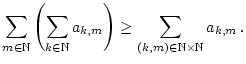 |
(1.3.6.5) |
Aus (1.3.6.2) und (1.3.6.4)
folgt die erste (und auf gleichem Wege auch die zweite) Identität
in (1.3.6.1).
Zum Abschluß bleibt zu zeigen, daß aus der Konvergenz der Reihe
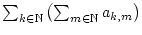 auch die Konvergenz von
auch die Konvergenz von
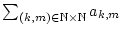 folgt. Angenommen, die Reihe
folgt. Angenommen, die Reihe
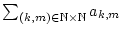 ist nicht konvergent. Dann divergiert diese bestimmt gegen
ist nicht konvergent. Dann divergiert diese bestimmt gegen 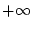 und für jedes
und für jedes
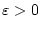 existiert ein
existiert ein
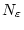 mit
mit
Ebenso wie in (1.3.6.3) sieht man, daß
und im Grenzwert
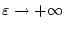 folgt die Divergenz
von
folgt die Divergenz
von
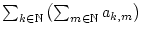 .
.




Next: Multiplikation von Reihen mit
Up: Der Umordnungssatz. Summierung über
Previous: Wichtige Eigenschaften von verallgemeinerten
Contents
2003-09-05
![]() und
und ![]() abzählbare Mengen, so ist
auch das kartesische Produkt
abzählbare Mengen, so ist
auch das kartesische Produkt ![]() abzählbar. Damit ist
für
abzählbar. Damit ist
für
![]() und
und
![]() ,
,
![]() ,
,
![]() , die Reihe
, die Reihe
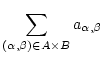
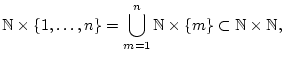
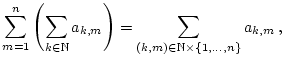
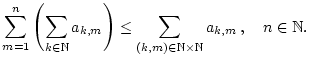
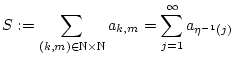
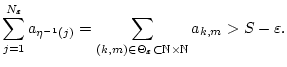
![]() auch die Konvergenz von
auch die Konvergenz von
![]() folgt. Angenommen, die Reihe
folgt. Angenommen, die Reihe
![]() ist nicht konvergent. Dann divergiert diese bestimmt gegen
ist nicht konvergent. Dann divergiert diese bestimmt gegen ![]() und für jedes
und für jedes
![]() existiert ein
existiert ein
![]() mit
mit