Es sei
![]() eine Folge und die
Funktion
eine Folge und die
Funktion
![]() sei auf jedem
Intervall
sei auf jedem
Intervall ![]() ,
, ![]() , integrierbar. Folgender Satz ist
nützlich für die praktische Untersuchung der Konvergenz von Reihen
und uneigentlichen Integralen:
, integrierbar. Folgender Satz ist
nützlich für die praktische Untersuchung der Konvergenz von Reihen
und uneigentlichen Integralen:
Konvergiert das uneigentliche Integral
![]() für gewisses
für gewisses ![]() , so konvergiert
, so konvergiert
![]() .
.
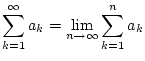 |
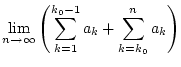 |
||
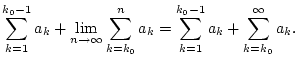 |