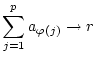Die Bedeutung des oben formulierten Umordnungssatzes unterstreicht
man am besten mit einem konträren Beispiel. Dazu betrachten wir eine
Folge reeller (positiver und negativer) Zahlen
![]() und setzen
und setzen
![]() sowie
sowie
![]() .
Dann gilt folgender Riemannscher Umordnungssatz für Reihen mit indefiniten
Summanden, nach dem man durch geeignete Umordnung der Summanden der
Reihe
.
Dann gilt folgender Riemannscher Umordnungssatz für Reihen mit indefiniten
Summanden, nach dem man durch geeignete Umordnung der Summanden der
Reihe
![]() jeden beliebigen
vorgegebenen Wert geben kann:
jeden beliebigen
vorgegebenen Wert geben kann:
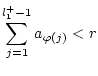
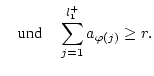
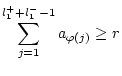
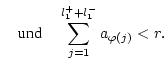
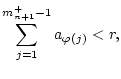 |
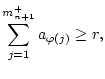 |
||
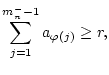 |
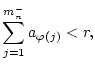 |
||
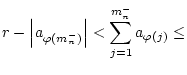 |
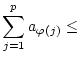 |
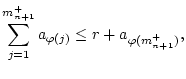 |
|
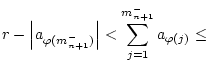 |
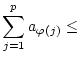 |
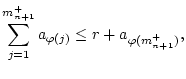 |