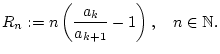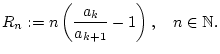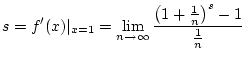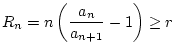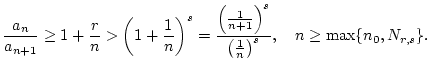Next: Das Kummersche Kriterium.
Up: Konvergenzkriterien für Reihen nichtnegativer
Previous: Es gibt keine universelle
Contents
Wegen dem Fehlen einer universellen Vergleichsfunktion wird jeder
auf dem Vergleichskriterium aufbauende Konvergenzsatz nur gewisse
Klassen von Reihen anwendbar sein. Die von uns formuliertenKonvergenzsätze
müssen daher gegebenenfalls verfeinert werden.
Ein Beispiel für eine solche Verfeinerung ist das Raabsche Kriterium.
 Wir zeigen zunächst, daß
Wir zeigen zunächst, daß
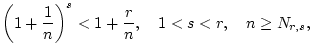 |
(1.4.6.1) |
für geeignetes
 . Dies folgt aus der Definition
der Ableitung der Funktion
. Dies folgt aus der Definition
der Ableitung der Funktion
 im Punkt
im Punkt 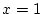 ,
denn
und damit wegen
,
denn
und damit wegen 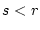 auch
auch
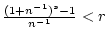 für
für
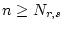 . Letzteres impliziert (1.4.6.1).
. Letzteres impliziert (1.4.6.1).
Nach Voraussetzung des Satzes gilt
Zusammen mit (1.4.6.1) folgt daraus
Die Konvergenz von
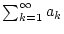 folgt nun aus
dem Vergleichskriterium Satz 1.4.1.3 mit
folgt nun aus
dem Vergleichskriterium Satz 1.4.1.3 mit
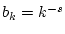 ,
da wie oben gezeigt die harmonische Reihe
,
da wie oben gezeigt die harmonische Reihe
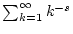 für
für 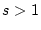 konvergiert.
konvergiert.

Aufgabe 1.4.6.2
Beweisen Sie die zweite Aussage des Satzes zur Divergenz!




Next: Das Kummersche Kriterium.
Up: Konvergenzkriterien für Reihen nichtnegativer
Previous: Es gibt keine universelle
Contents
2003-09-05