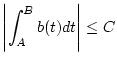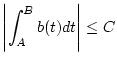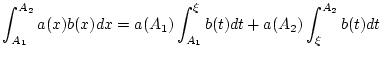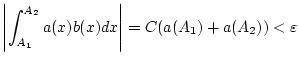Next: Unendliche Produkte
Up: Konvergenzkriterien für im Allgemeinen
Previous: Das Leibniz-Kriterium für alternierende
Contents
 Wir wenden das Cauchy-Kriterium des Satzes 1.2.1.2
zur Konvergenz uneigentlicher Integrale an. Nach dem zweiten Mittelwertsatz
der Integralrechnung gilt
für geeignetes
Wir wenden das Cauchy-Kriterium des Satzes 1.2.1.2
zur Konvergenz uneigentlicher Integrale an. Nach dem zweiten Mittelwertsatz
der Integralrechnung gilt
für geeignetes
![$ \xi \in [A_{1},A_{2}] $](img727.png) . Da der Absolutbetrag
der beiden Integrale
. Da der Absolutbetrag
der beiden Integrale
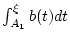 sowie
sowie
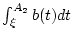 durch die Konstante
durch die Konstante 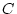 beschränkt ist und da weiterhin
beschränkt ist und da weiterhin 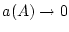 für
für
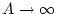 , so folgt für beliebiges
, so folgt für beliebiges
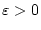 für alle
für alle
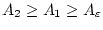 . Dies entspricht
dem Cauchy-Kriterium für uneigentliche Integrale.
. Dies entspricht
dem Cauchy-Kriterium für uneigentliche Integrale.

2003-09-05