



Next: Das Kriterium von Dirichlet
Up: Konvergenzkriterien für im Allgemeinen
Previous: Das Kriterium von Dirichlet.
Contents
Satz 1.7.4.1
Es sei
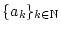 eine monoton fallende Folge
positiver Zahlen, welche gegen Null konvergiert. Dann ist die Reihe
eine monoton fallende Folge
positiver Zahlen, welche gegen Null konvergiert. Dann ist die Reihe
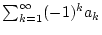 bedingt konvergent.
bedingt konvergent.
 Der Satz folgt aus dem Kriterium von Dirichlet mit
Der Satz folgt aus dem Kriterium von Dirichlet mit
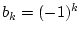 ,
da dann die Folge
,
da dann die Folge
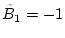 ,
,
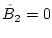 ,
,
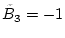 usw. beschränkt ist.
usw. beschränkt ist.

2003-09-05