Der Umordnungssatz für absolut konvergente Reihen.

Für absolut konvergente Reihen gilt der Umordnungssatz: Konvergenz und Wert der Reihe sind unabhängig von der Ordnung der Summanden.

Satz 1.6.4.1   Es sei $a_{k}\in \mathbb{K}^{p}$ für $k\in \mathbb{N}$ und $\varphi :\mathbb{N}\to \mathbb{N}$ sei eine Umordnung (eine bijektive Abbildung auf $\mathbb{N}$). Konvergiert die Reihe $\sum _{k=1}^{\infty }a_{k}$ absolut, so konvergiert auch die Reihe $\sum _{k=1}^{\infty }a_{\varphi (k)}$ absolut und es gilt

$$\sum _{k=1}^{\infty }a_{k}=\sum _{k=1}^{\infty }a_{\varphi (k)}.$$ (1.6.4.1)

$\blacktriangleright$ Nach dem Umordnungssatz 1.3.2.1 für Reihen mit nichtnegativen Summanden konvergieren $\sum _{k=1}^{\infty }\parallel a_{k}\parallel$ und $\sum _{k=1}^{\infty }\parallel a_{\varphi (k)}\parallel$ gleichzeitig; damit sind die Reihen $\sum _{k=1}^{\infty }a_{k}$ und $\sum _{k=1}^{\infty }a_{\varphi (k)}$ gleichzeitig absolut konvergent.

Wir betrachten zunächst den Fall $a_{k}\in \mathbb{R}$. Angenommen, die Reihe $\sum _{k=1}^{\infty }a_{k}$ konvergiert absolut. Nach Satz 1.6.3.6 konvergieren damit auch $\sum _{k=1}^{\infty }a_{k}^{+}$ und $\sum _{k-1}^{\infty }a_{k}^{-}$. Auf diese Reihen ist Satz 1.3.2.1 anwendbar und es gilt

$$\sum _{k=1}^{\infty }a_{k}^{+}=\sum _{k=1}^{\infty }a_{\varphi (k... ...,\quad \sum _{k-1}^{\infty }a_{k}^{-}=\sum _{k-1}^{\infty }a_{\varphi (k)}^{-}.$$

Da offensichtlich $(a_{\varphi (k)})^{+}=a_{\varphi (k)}^{+}$ und $(a_{\varphi (k)})^{-}=a_{\varphi (k)}^{-}$ sowie $a_{k}=a_{k}^{+}-a_{k}^{-}$ als auch $a_{\varphi (k)}=(a_{\varphi (k)})^{+}-(a_{\varphi (k)})^{-}$ für alle $k\in \mathbb{N}$, so gilt nach Satz 1.2.3.1

$$\sum _{k=1}^{\infty }a_{k} = \sum _{k=1}^{\infty }a_{k}^{+}-\sum _{k=1}^{\infty }a_{k}^{-}=\sum _{k=1}^{\infty }a_{\varphi (k)}^{+}-\sum _{k-1}^{\infty }a_{\varphi (k)}^{-}$$

$$= \sum _{k=1}^{\infty }(a_{\varphi (k)})^{+}-\sum _{k-1}^{\infty }(a_{\varphi (k)})^{-}=\sum _{k=1}^{\infty }a_{\varphi (k)}.$$

Im allgemeine Fall $a_{k}\in \mathbb{K}^{p}$ folgt die Identität (1.6.4.1) nun komponentenweise aus Satz 1.6.3.3 und 1.6.3.4. $\blacktriangleleft$

Beispiel 1.6.4.2   Die Riemannsche Zetafunktion. Wir untersuchen die Reihe

$$\zeta (s)=\sum _{n=1}^{\infty }\frac{1}{n^{s}},\quad s\in \mathbb{C},$$

auf absolute Konvergenz. mit der Notation $s=\sigma +it$, $\sigma =\Re s$, $t=\Im s$ gilt

$$\vert n^{-s}\vert=\frac{1}{\vert n^{\sigma +it}\vert}=\frac{1}{\vert n^{\sigma }\vert\vert n^{it}\vert}=n^{-\sigma }.$$

Da die harmonische Reihe $\sum _{n=1}^{\infty }n^{-\sigma }$, $\sigma \in \mathbb{R}$ für $\sigma >1$ konvergiert, so ist die Reihe $\sum _{n=1}^{\infty }n^{-s}$, $s\in \mathbb{C}$, für $\Re s=\sigma >1$ absolut konvergent.

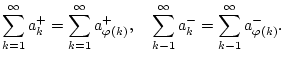
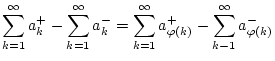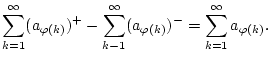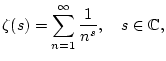
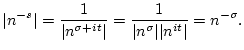
Die Riemannschen Zetafunktion $\zeta (s)$ spielt in den verschiedensten mathematischen Teilgebieten eine zentrale Rolle. Mit ihr ist auch das wohl gegenwärtig berühmteste offene mathematische Problem verbunden, nachdem alle Nullstellen dieser Funktion auf der Gerade $\sigma =Res=\frac{1}{2}$ liegen. Dies ist eines der sieben sogenannten Millenium-Probleme, für deren Lösung das Clay Mathematics Institute einen Preis von jeweils 1.000.000 US$ ausgeschrieben hat.