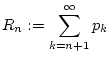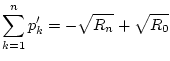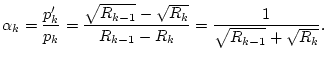Für jede divergente Reihe
![]() positiver
Glieder kann man eine gegen Null konvergente Folge positiver Zahlen
positiver
Glieder kann man eine gegen Null konvergente Folge positiver Zahlen
![]() finden, so daß die Reihe
finden, so daß die Reihe
![]() ebenfalls divergiert.
ebenfalls divergiert.
Das Vergleichskriterium führt auf die Frage, ob eine universelle Vergleichsfolge existiert, an Hand derer man über die Konvergenz jeder gegebenen Reihe nichtnegativer Summanden entscheiden kann. Der folgende Satz beantwortet diese Frage negativ:
Für jede divergente Reihe
![]() positiver
Glieder kann man eine gegen Null konvergente Folge positiver Zahlen
positiver
Glieder kann man eine gegen Null konvergente Folge positiver Zahlen
![]() finden, so daß die Reihe
finden, so daß die Reihe
![]() ebenfalls divergiert.
ebenfalls divergiert.